filmov
tv
Solving a Trigonometric System with Tangents
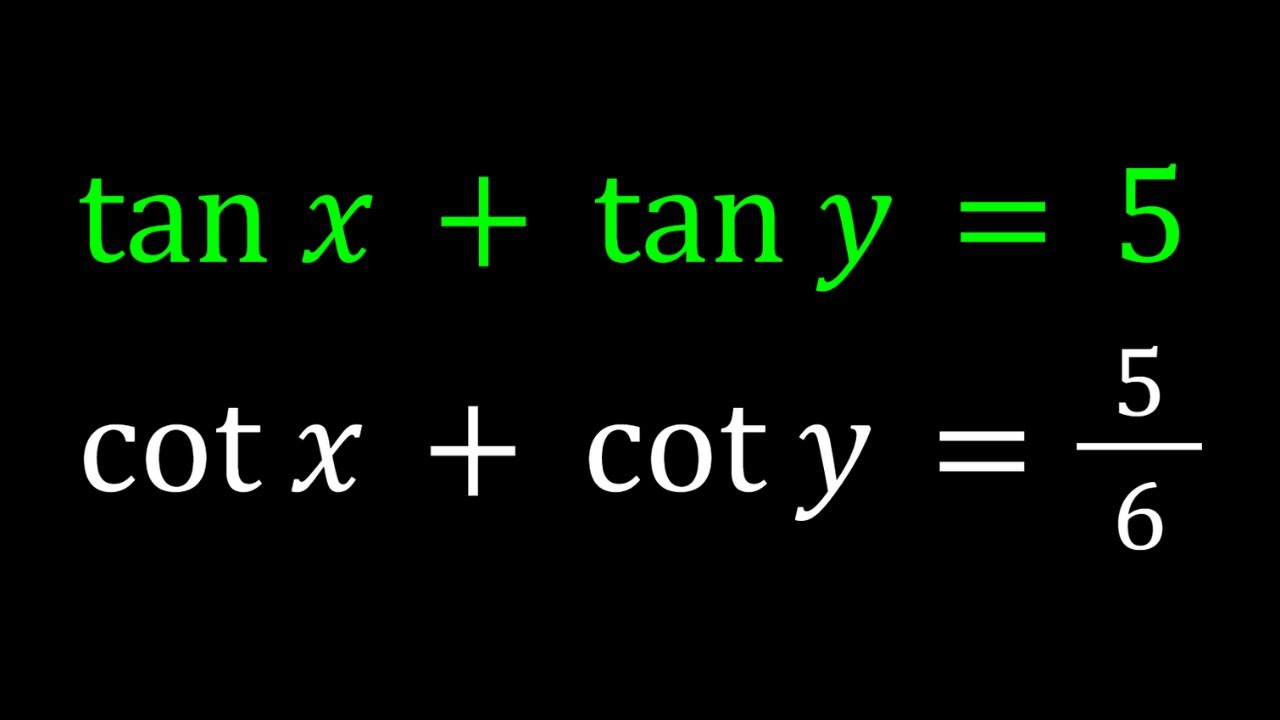
Показать описание
If you need to post a picture of your solution or idea:
#TrigonometryProblems #TrigonometricSystems
PLAYLISTS 🎵 :
#TrigonometryProblems #TrigonometricSystems
PLAYLISTS 🎵 :
Solving a Trigonometric System with Tangents
Trigonometric System of Equations
Solving Trigonometric Equations
A Linear Trigonometric System
A Quick and Easy Trigonometric System
An Introduction to Solving Trigonometric Equations
How to Solve Trigonometric Equations (Precalculus - Trigonometry 22)
Classwiz How-To: Solving a Trigonometric Equation
TRIGONOMETRY in 1 Shot | All Concepts Covered | JEE Mains and Advanced | JEE 2025
Solving Trigonometric Equations | A-level Mathematics
Solve sin=2/5 Trigonometric equation
Solving Trigonometric Equations - How to Write General Solution
Solving Trigonometric Equations by Quadrants (1 of 3: Introduction)
How to solve a trigonometric equation with sine and cosine
Find the solutions to a trig equation between 0 and 2pi
Solving Trigonometric Equations
Solving Trigonometric Equations (1 of 5: Overview)
Solving a trig function with sine and cosine
Solving Trigonometric Equations I
How to apply factoring to solve a trigonometric equation
Solving Trigonometric Equations By Factoring & By Using Double Angle Identities
Y10 Review Questions (Solving trigonometric equations with quadrants)
Solve the Trigonometric system of equations | College Entrance Exam
Solving Trigonometric Equations Multiple Angles
Комментарии
 0:08:32
0:08:32
 0:07:26
0:07:26
 0:15:22
0:15:22
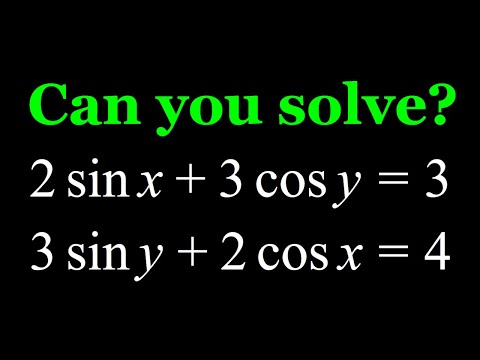 0:09:31
0:09:31
 0:09:58
0:09:58
 0:14:17
0:14:17
 1:34:36
1:34:36
 0:03:33
0:03:33
 2:54:28
2:54:28
 0:38:12
0:38:12
 0:04:04
0:04:04
 0:06:26
0:06:26
 0:04:42
0:04:42
 0:07:00
0:07:00
 0:03:38
0:03:38
 0:15:47
0:15:47
 0:06:38
0:06:38
 0:07:00
0:07:00
 0:08:19
0:08:19
 0:10:34
0:10:34
 0:18:32
0:18:32
 0:07:07
0:07:07
 0:04:07
0:04:07
 0:09:57
0:09:57