filmov
tv
Solving Trigonometric Equations | A-level Mathematics
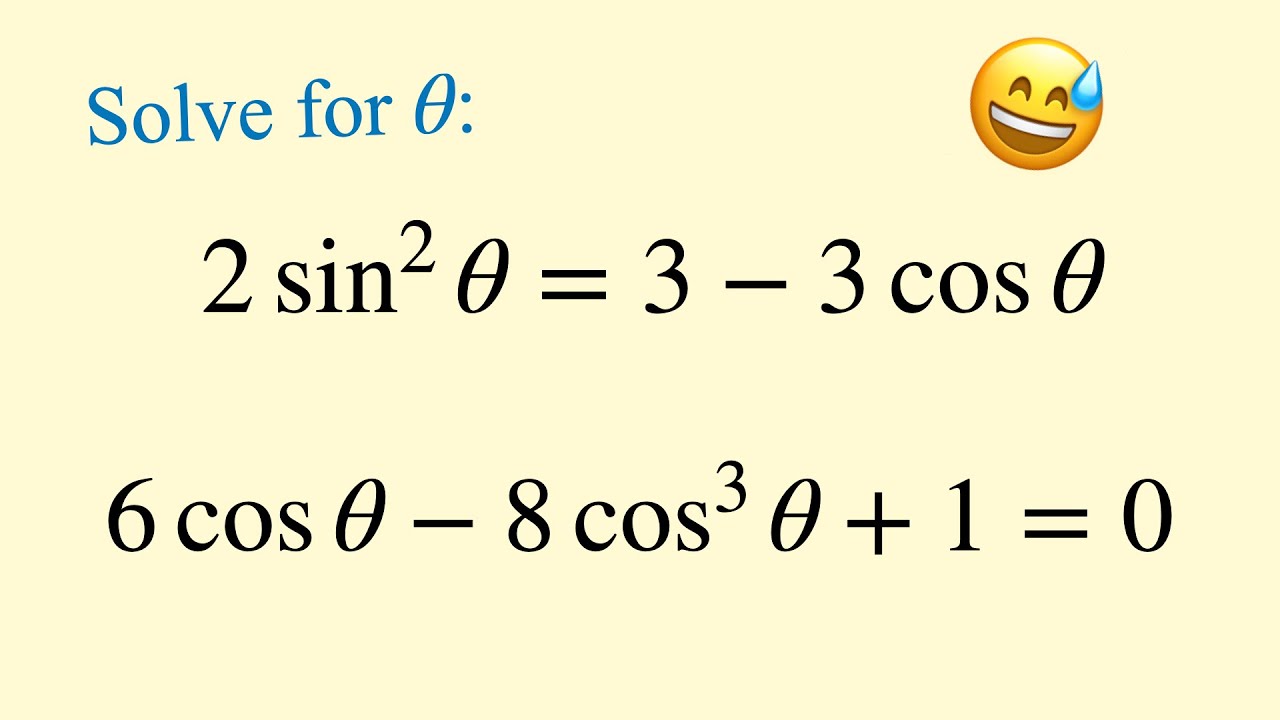
Показать описание
Solving trigonometric equations - from the basics to more challenging problems. This is a large topic but with practice and a good understanding of the fundamentals you can master it quickly.
*At 11:53 the interval should be for x, not theta
❤️ ❤️ ❤️ Support the channel ❤️ ❤️ ❤️
00:00 intro
00:58 Level 1 equations
11:19 Level 2 equations
23:49 Level 3 equations
*At 11:53 the interval should be for x, not theta
❤️ ❤️ ❤️ Support the channel ❤️ ❤️ ❤️
00:00 intro
00:58 Level 1 equations
11:19 Level 2 equations
23:49 Level 3 equations
Edexcel A level Maths: 7.4 Solving Trigonometric Equations
Solving Trigonometric Equations | A-level Mathematics
All of Trigonometric Identities and Equations in 30 minutes!! | Chapter 10 | A level Pure Maths
A-Level Maths: E7-07 [Trig Equations: Solving Basic Trigonometric Equations in degrees]
Edexcel AS Level Maths: 10.4 Solving Trigonometric Equations (Simple Trigonometric Equations)
Solving Trigonometric Equations
Solving Trigonometric Equations By Finding All Solutions
A-Level Maths: E7-27 [Trig Equations: Solve sin(2x) = 0.8 between 0 and 360 degrees]
Solving Trigonometric Equations - How to Write General Solution
Solving simple trig equations
Day 20: Solving Trig Equations • 100 Days of A-Level Maths 🧮
Solving Trigonometric Equations
Find the solutions to a trig equation between 0 and 2pi
How to Solve Trigonometric Equations (Precalculus - Trigonometry 22)
Solving Trigonometric Equations w/sec, cosec, cot - A-Level Maths
An Introduction to Solving Trigonometric Equations
Pure 2 Chapter 6 Trigonometric Identities and Equations A-level Mathematics International
3.8.1 Solving trigonometric equations | IB math AA | Mr. Flynn IB
How to use CAST diagrams to solve Trigonometric Equations - Year 1 A Level Maths
Trigonometric Equations | A-level Maths | OCR, AQA, Edexcel
Solving Trigonometric Equations 1
AS Maths - Pure - Harder Trigonometric Equations
A-Level Maths: E7-21 [Trig Equations: Solve sin(x + 65) = 0.7 between 0 and 360 degrees]
Edexcel AS Level Maths: 10.5 Harder Trigonometric Equations (Solving using CAST diagram)
Комментарии
 0:09:03
0:09:03
 0:38:12
0:38:12
 0:36:35
0:36:35
 0:10:01
0:10:01
 0:08:39
0:08:39
 0:15:22
0:15:22
 0:11:49
0:11:49
 0:04:12
0:04:12
 0:06:26
0:06:26
 0:06:28
0:06:28
 0:00:39
0:00:39
 0:15:47
0:15:47
 0:03:38
0:03:38
 1:34:36
1:34:36
 0:19:27
0:19:27
 0:14:17
0:14:17
 1:36:45
1:36:45
 0:12:51
0:12:51
 0:15:25
0:15:25
 0:22:05
0:22:05
 0:13:47
0:13:47
 0:13:17
0:13:17
 0:06:48
0:06:48
 0:16:50
0:16:50