filmov
tv
Finding the Minimum Value of a Complex Expression Using AM-GM Inequality
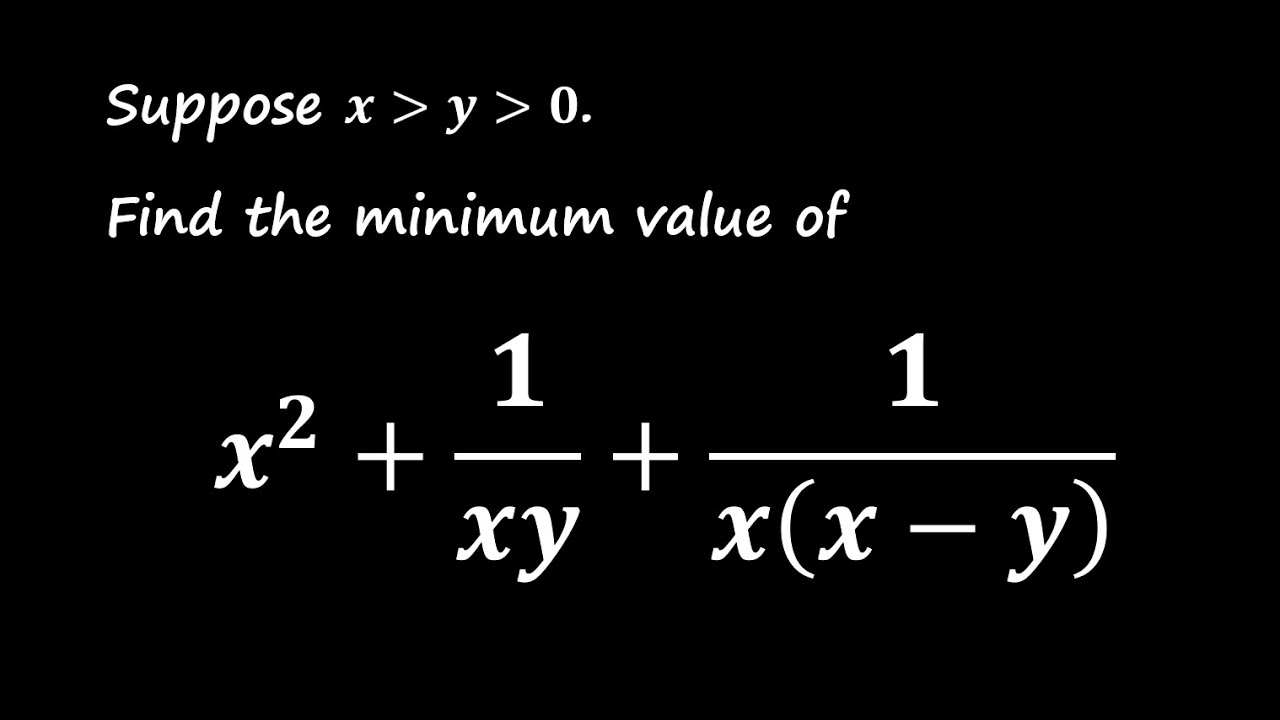
Показать описание
In this video, we explore how to find the minimum value of the expression. x² + 1/xy + 1/(x²-xy), where x,y positive. We use the powerful Arithmetic Mean-Geometric Mean inequality to break down the problem step-by-step. Follow along as we simplify the expression, apply the inequality, and solve for the conditions that give us the minimum value. Whether you're preparing for a math competition or just want to sharpen your problem-solving skills, this video will walk you through the process in a clear and detailed way. Don't forget to like, share, and subscribe for more math problem-solving content!
Determine if a quadratic has a max or min value then find it (mistake)
How to Find the Maximum or Minimum Value of a Quadratic Function Easily
Finding Local Maximum and Minimum Values of a Function - Relative Extrema
How to Find the Maximum or Minimum Value of Quadratic Functions
Finding Local Maxima and Minima by Differentiation
Maximum and Minimum Values of a Quadratic Function
Minimum Value of A Function #maths #algebra #math
How To Find The Minimum (Smallest) Value (In A Data Set) Using The MIN Function In Excel Explained
Finding the Minimum Value (AM-GM): 2024 Austrian Regional Competition Solution
Finding Absolute Maximum and Minimum Values - Absolute Extrema
Identifying The Relative Maximum and Minimum Values of a Function
Learning to determine the minimum value of an objective function
Excel Find the Min and Max Value in a Column using Conditional Formatting
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Maximum and Minimum Value Word Problems - Quadratic Equations
How to find the Maximum and Minimum value of Quadratic Function
Absolute Maximum & Minimum
4 Methods to Find Minimum Value From Quadratic Equation
Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus
Learning how to find the maximum value of an objective function
Finding the Minimum or Maximum of Quadratic Functions
❖ Maximum and Minimum Values of Quadratic Functions ❖
How do I find the maximum and minimum values of f on a given domain? - Week 8 - Lecture 2 - Mooculus
How to find the Maximum/Minimum of a Quadratic Function in 5 different ways
Комментарии
 0:04:54
0:04:54
 0:02:59
0:02:59
 0:14:18
0:14:18
 0:04:55
0:04:55
 0:06:17
0:06:17
 0:06:20
0:06:20
 0:00:47
0:00:47
 0:00:53
0:00:53
 0:03:53
0:03:53
 0:17:17
0:17:17
 0:03:47
0:03:47
 0:03:59
0:03:59
 0:04:32
0:04:32
 0:11:24
0:11:24
 0:05:58
0:05:58
 0:07:27
0:07:27
 0:01:00
0:01:00
 0:09:52
0:09:52
 0:09:15
0:09:15
 0:09:00
0:09:00
 0:07:22
0:07:22
 0:04:28
0:04:28
 0:09:07
0:09:07
 0:08:29
0:08:29