filmov
tv
Abel's brilliant trick for solving differential equations
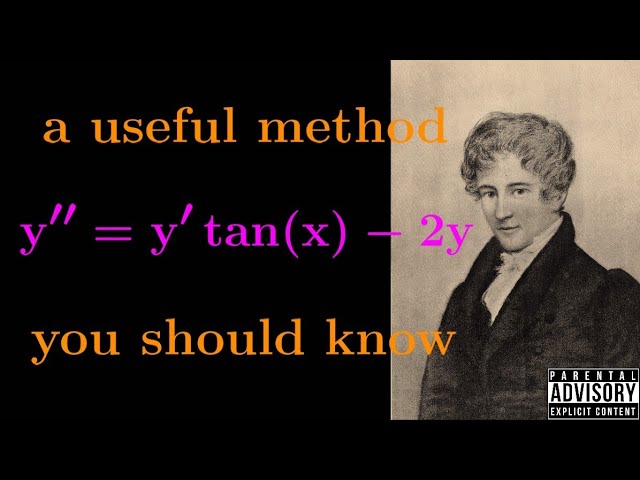
Показать описание
Abel's method is an interesting approach to solving 2nd order linear differential equations using the Wronskian. Here's a nice example of its application.
My complex analysis lectures:
If you like the videos and would like to support the channel:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
My complex analysis lectures:
If you like the videos and would like to support the channel:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
Abel's brilliant trick for solving differential equations
Putin flirts, Putin sigma rule, Putin body language #sigma #confidence #bodylanguage #putin #shorts
The Tits alternative for the automorphism group of a free product (GGD/GEAR Seminar)
'Why I Fire People Every Day' - Warren Buffett
Edward Witten Epic Reply 🤣 Destroys String Theory Dissenters
New Skip BREAKS Mario Kart DS After 18 Years
Tukka Maarna Seekho🔥🔥🔥| Tricks & Cheat Codes #324 [Course Links In Description]
Group and Abelian Group
Mysterio Reveal Scene | SPIDER-MAN FAR FROM HOME (2019) Movie CLIP HD
EVERY SECRET in Brookhaven Roblox
5 Issues That Cause Skipped Stitches - Your Best Solution is Here
The Abel Prize announcement 2022
How to Download Embedded Videos Using DevTools
Teaching myself abstract algebra
Boy Hides His Power even being Mocked until his Family Asks for Help to Become King | Manga Recap
Betrayals, Duels, Love Triangles and Polynomials
Top 20 Worst TV Shows of the Century (So Far)
8 Real Signs of Highly Intelligent People - Zaheen logon ki nishaniyan - Genius People Signs
2017 Personality 22: Conclusion: Psychology and Belief
Teamwork Wins! 🏈 | Gecko's Garage 🚚 | Cartoons For Kids | Toddler Fun Learning
James Clerk Maxwell’s Influence on Mathematics | Sir Michael Atiyah
complex ionic equation - Redox 3 by chellphick
How I Came to Terms with Complex Numbers
IHI Forum 2021 Keynote Address - Kedar S. Mate, MD: The Trust Triangle
Комментарии
 0:12:28
0:12:28
 0:00:20
0:00:20
 0:53:55
0:53:55
 0:04:23
0:04:23
 0:01:42
0:01:42
 0:11:38
0:11:38
 0:12:49
0:12:49
 0:10:44
0:10:44
 0:04:29
0:04:29
 1:25:02
1:25:02
 0:02:54
0:02:54
 0:25:51
0:25:51
 0:02:27
0:02:27
 0:14:41
0:14:41
 1:25:11
1:25:11
 0:13:57
0:13:57
 0:23:33
0:23:33
 0:09:52
0:09:52
 1:08:29
1:08:29
 1:58:22
1:58:22
 0:29:25
0:29:25
 0:54:22
0:54:22
 1:22:47
1:22:47
 0:48:45
0:48:45