Group and Abelian Group

Показать описание

Network Security: Group and Abelian Group
Topics discussed:
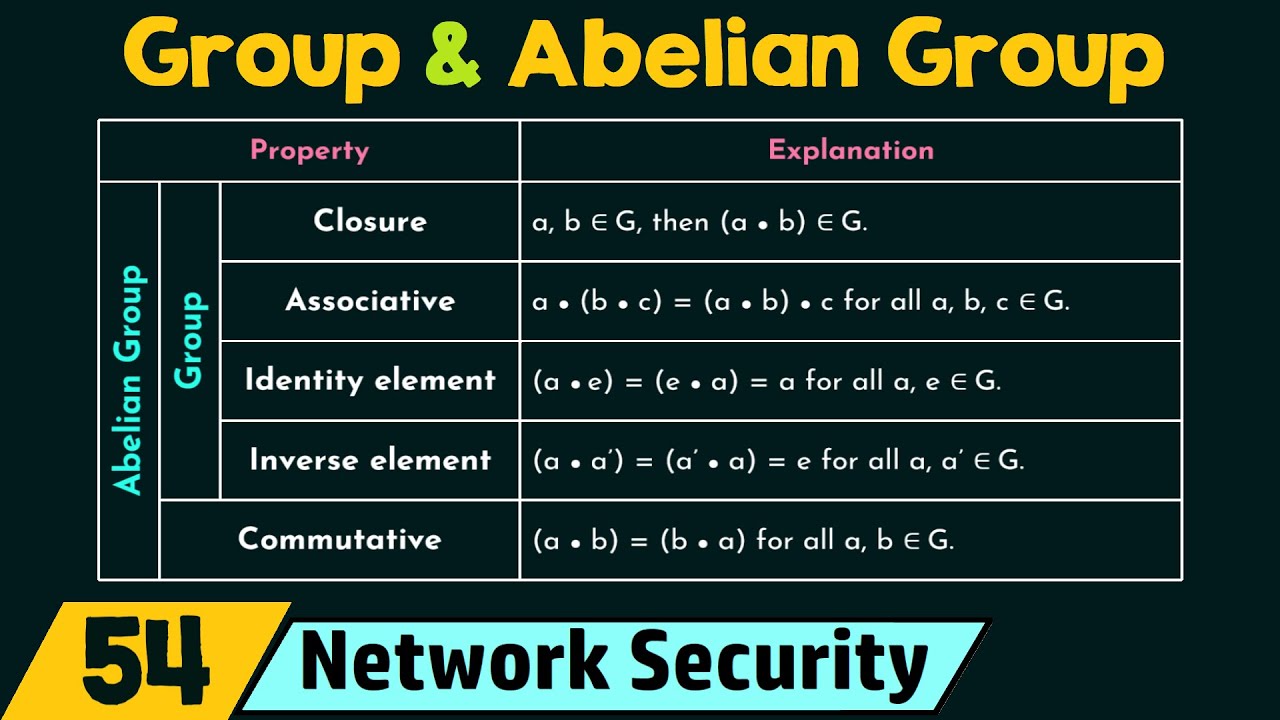
1) The definition of group and abelian group.
2) Properties to be satisfied for the set of elements to be a group and abelian group.
3) Explanation on closure, associative, identity, inverse, and commutative properties.
4) Solved problem of determining (Z, +) a group and abelian group.
5) Various mathematical notations for a set of numbers in number theory.

Music:
Axol x Alex Skrindo - You [NCS Release]

#NetworkSecurityByNeso #Cryptography #NetworkSecurity #Group #AbelianGroup

Рекомендации по теме

Комментарии

Home work question given at 10:13 is not a group as 3 + (-3) = 0 and 0 is not the Z'. So its not closed with addition operation.

bilaljan

Beautifully explained with such a direct approach. Loved it.

arskas

Thanks a lot for this explanation. It was all going over my head while learning vector space. Now I'll be able to understand it all.

NishithSavla

Beautiful explanation ...In Closure property, 5-2=3

luckieboy_logee

You did a fantastic job with this topic. Thank you.

valeriereid

Thankyouu so much sir for that cain short cut ❤ the whole video is amazing

Sammie

Really smooth explanation. Understood with just one watch. 🥇🏆🏅

erolakkas

Very clearly explained, thanks so much!

williesanape

Sir your videos are really intelligible and I liked them very much .Could u please upload the videos in a faster rate? I am so eager to learn the whole subject

donthusravya

For the 1st time I understood this topic very well

photolab

very well explained. thank you for all the help.

simpleandminimalmaybe

That was helpful...do one for binary operations

DumolwenkosiVhumbunu

very clear and useful!! many thanks; ❤️

AlessandroZir

Sir in closure property a=5, b=-2 then it is 3 not -3 sir...

adhityaadhi

and i want more videos from you with fields odered fields because those are the concepts i am stuck with

nightmare

damn, too good presentation & explanation man, please keep up the good work.

mahadihassanriyadh

6:09 it should be 3 not -3. But it is good and comprehensible presentation 👏👏

Math-yzgs

thank you so much it was an amazing explanation

MohaMohamoud-rd

Answer to H.W :

Z* = {... -3, -2, -1, 1, 2, 3 ...} under Addition.

Closure => Any Two Numbers : -1, 1 ∈ Z* but -1 + 1 = 0 ∉ Z*

Since, one of the property out of CAIN is not satisfied. Hence, (Z*, +) is not Group. Right ?

rajeshprajapati

Hw answer

Z+ --> set of positive integers
Identity -->0 ( identity elmt in addition)

Consider inverse property..
Since z+ consists of all positive integers, obviously sum of any two elements won't give identity elmt 0. So each element in z+ does not have a corresponding inverse ---> violation of CAIN ---> hence { Z+, +} not a group

aakashjason

Group and Abelian Group

Group and Abelian Group

Group Definition (expanded) - Abstract Algebra

Abelian Group Problem 1 - Algebraic Structures - Discrete Mathematics

(Abstract Algebra 1) Definition of an Abelian Group

Cryptography and Network Security- Group and Abelian group

Every Cyclic Group is Abelian | Abstract Algebra

Abelian Group in Discrete Mathematics with examples

Every Cyclic Group is Abelian Proof

Group Theory ( QUESTION- 17 ) | Algebra | BSc 2nd Year | HPU

(Abstract Algebra 1) Cyclic Groups and Abelian Groups

Abstract Algebra 18: Abelian groups

AlgTopReview4: Free abelian groups and non-commutative groups

Abstract Algebra : What is a Group and an Abelian Group? (Semigroup and Monoid) (In Tagalog)

show that (z,+) is an abelian group , (z,+) is abelian group theory

3. Group || Abelian Group || Examples of Group || Examples of not a group

abelian and non abelian group|| communative group and abelian group is same ||

Group Theory | Group | Abelian Group | Lecture 7| Theta Classes

Group Theory | Examples Of Group & Abelian Group | Discrete Mathematics

Abelian Group Problem 3 - Algebraic Structures - Discrete Mathematics

#07 how to check group is non abelian or abelian group | group of order 55 is abelian or non abelian

What is an abelian group/commutative group

#19 Which of the abelian and non-abelian group of order 5,9,15 and 10 ?

Visual Group Theory, Lecture 2.1: Cyclic and abelian groups

Abelian and Non- abelian groups with example