filmov
tv
Calculus: Absolute Maximum Minimum for Polynomial First Derivative Application

Показать описание
Absolute Maximum and Absolute minimum value for any function continuous in closed interval [a, b] will always exist at the critical numbers or at the end points.
Check the value of the function at the critical numbers and at the end-points to find the result.
Steps to find increasing and decreasing interval of any function, f(x), are:
find the first derivative, f'(x)
find critical numbers, f'(x) = 0 or does not exist (DNE)
INTERVAL TABLE TEST:
These critical numbers divide the domain in intervals. Test each interval with a test point.
RESULT:
If f'(x) is greater than 0 then f(x) is increasing.
If f'(x) is less than 0 then f(x) is decreasing.
#calculus #derivativeapplication #increasinginterval #decreasinginterval #mcv4u #anilkumar #globalmathinstitute #absolutemaximum #absoluteminimum
Check the value of the function at the critical numbers and at the end-points to find the result.
Steps to find increasing and decreasing interval of any function, f(x), are:
find the first derivative, f'(x)
find critical numbers, f'(x) = 0 or does not exist (DNE)
INTERVAL TABLE TEST:
These critical numbers divide the domain in intervals. Test each interval with a test point.
RESULT:
If f'(x) is greater than 0 then f(x) is increasing.
If f'(x) is less than 0 then f(x) is decreasing.
#calculus #derivativeapplication #increasinginterval #decreasinginterval #mcv4u #anilkumar #globalmathinstitute #absolutemaximum #absoluteminimum
Finding Absolute Maximum and Minimum Values - Absolute Extrema
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Absolute minima & maxima (entire domain) | AP Calculus AB | Khan Academy
Absolute Maximum/Minimum Values of Multivariable Functions - Part 1 of 2
Calculus: Absolute Maximum and Minimum Values
Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus
Calculus Absolute Maximum Minimum Things to Remember
Local and Absolute Maximum and Minimum from a Graph
Engineering Mathematics 11 | Multiple Integrals 2.0 (Part 03) | All Branches
Calculus: Absolute Maximum Minimum for Polynomial First Derivative Application
Local and Absolute Maximum Minimum Differences
finding the absolute minimum and maximum of a trigonometric function
Calculus 1: Maximum & Minimum Values Part 1 (Section 4.1) | Math with Professor V
Learn how to find the absolute max, min and relative max min of a graph
Absolute max and min values Problem 1 (Multivariable Calculus)
Calculus 3 Lecture 13.8: Finding Extrema of Functions of 2 Variables (Max and Min)
Absolute Maximum for Trigonometric Function Calculus Extreme Value Theorem
Video3166 - Calculus 3 - Absolute Maximum/Minimum - Bounded Region - Part 1/2
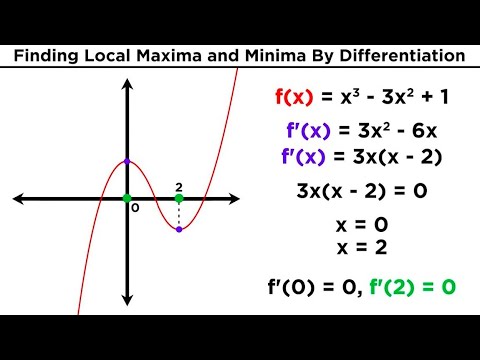
Finding Local Maxima and Minima by Differentiation
The Closed Interval Method to Find Absolute Maximums and Minimums
Finding Local Maximum and Minimum Values of a Function - Relative Extrema
Calculus I: Absolute max and min (log function)
Global Maximum and Minimum
Calculus 3: Maximum and Minimum Values (Video #17) | Math with Professor V
Комментарии
 0:17:17
0:17:17
 0:11:24
0:11:24
 0:09:23
0:09:23
 0:06:18
0:06:18
 0:03:05
0:03:05
 0:09:15
0:09:15
 0:08:34
0:08:34
 0:03:27
0:03:27
 1:36:03
1:36:03
 0:05:21
0:05:21
 0:08:34
0:08:34
 0:09:18
0:09:18
 0:18:57
0:18:57
 0:02:41
0:02:41
 0:25:26
0:25:26
 3:38:16
3:38:16
 0:06:42
0:06:42
 0:11:10
0:11:10
 0:06:17
0:06:17
 0:08:51
0:08:51
 0:14:18
0:14:18
 0:05:55
0:05:55
 0:04:31
0:04:31
 1:05:35
1:05:35