filmov
tv
Proof that sum(sin(n)/n) Converges using Dirichlet's Test

Показать описание
Proof that sum(sin(n)/n) Converges using Dirichlet's Test
Proof that sum(sin(n)/n) Converges using Dirichlet's Test
The Sequence a_n = sin(n)/n Converges or Diverges Two Solutions with Proof
checking for absolute convergence, series of sin(2n)/(1+2^n), calculus 2 tutorial
using complex numbers to evaluate the sum of sin(n)/n
How to Prove the Squence a_n = sin(n)/sqrt(n) Converges using the Squeeze Theorem
Using Abel's Test to Prove a Fourier Sine Series Converges
Determine whether series converges or diverges (ln n)/n. Use appropriate test
incredible sin sin sum
sum of sin n/n^2 converges or diverges?
How to Determine if a Sequence Converges or Diverges: Example with n*sin(1/n)
the sum of sin(n)/n by using the Fourier Series (fourier series engineering mathematics)
Proof: Limit Law for Sum of Convergent Sequences | Real Analysis
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Every Student Should See This
Series sin(1/n) diverges
Determine if series converges or diverges. {sin(1/n)}. Limit Comparison Test with harmonic series
Show that the series converges absolutely (2(sin x)^n)/(n! +3). Ratio Test
Does sum 1/n^2 converge? - Week 2 - Lecture 11 - Sequences and Series
how to use the ratio test for the series of n!/n^n
Determining whether a sequence converges or diverges
Does Sum(sin^3(1/n)) Converge or Diverge?
Determine if series is absolutely, conditionally convergent or divergent (cos n pi)/n
Determine if sequence converges or diverges. If converges find limit. {(n sin n)/(n^2 +1)}
Converging and Diverging Sequences Using Limits - Practice Problems
Комментарии
 0:10:56
0:10:56
 0:02:47
0:02:47
 0:05:36
0:05:36
 0:11:31
0:11:31
 0:02:28
0:02:28
 0:06:41
0:06:41
 0:01:52
0:01:52
 0:02:49
0:02:49
 0:05:05
0:05:05
 0:04:04
0:04:04
 0:08:27
0:08:27
 0:07:56
0:07:56
 0:05:36
0:05:36
 0:00:58
0:00:58
 0:05:33
0:05:33
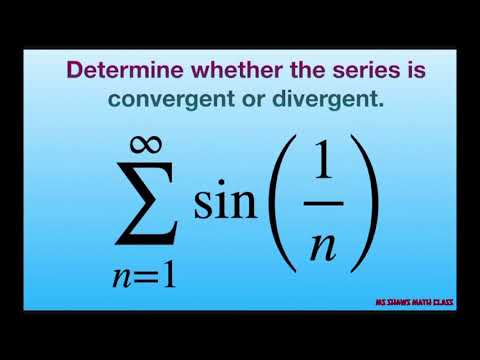 0:04:07
0:04:07
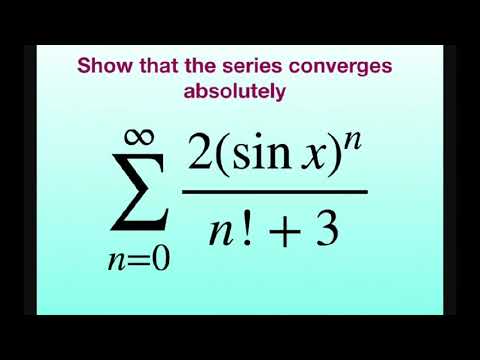 0:03:43
0:03:43
 0:09:01
0:09:01
 0:08:26
0:08:26
 0:05:39
0:05:39
 0:04:17
0:04:17
 0:03:11
0:03:11
 0:02:18
0:02:18
 0:30:13
0:30:13