Proof: Limit Law for Sum of Convergent Sequences | Real Analysis

preview_player
Показать описание
We prove the limit law for the sum of convergent sequences. If a_n converges to a and b_n converges to b, then the sequence a_n + b_n converges to a + b. As in, the sum of convergent sequences converges to the sum of their limits. This is a fairly straightforward proof using the epsilon definition of a convergent sequence.

★DONATE★

Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Limit Laws - 0:08:18

Limit Laws - Proof of Sum Law

Proof: Limit Law 0:07:24

Proof: Limit Law for Sum of Convergent Series | Real Analysis

Proof: Limit Law 0:07:56

Proof: Limit Law for Sum of Convergent Sequences | Real Analysis

Limits: Sum Law 0:02:35

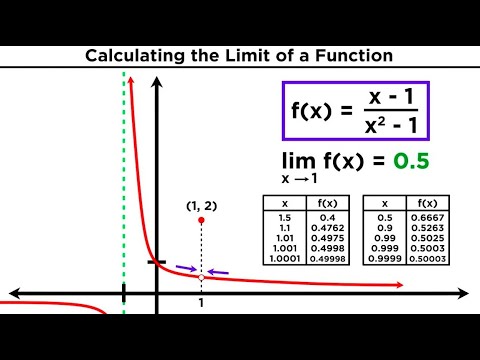
Limits: Sum Law

Proof of Sum 0:07:19

Proof of Sum Law (Limit Laws)

Proof of the 0:12:06

Proof of the Sum Law for Limits

Advanced Calculus Sum 0:05:15

Advanced Calculus Sum of Limits Delta-Epsilon Proof

Proof of a 0:09:17

Proof of a Limit Value Using Epsilon and Delta

Sum Law for 0:29:56

Sum Law for limits

Sum of limits 0:05:40

Sum of limits

Sum Law for 0:11:38

Sum Law for Limits of Complex Functions

* PROOF 10: 0:04:41

* PROOF 10: Limit of a Sum of Sequences (case of finite limits)

Proof of the 0:07:04

Proof of the Sum Rule for Limit of Sequences

Prove first limit 0:11:56

Prove first limit law, limit of a sum is the sum of the limits

* PROOF 13: 0:04:31

* PROOF 13: Limit of a sum of functions (case of finite limits)

Limits and Limit 0:12:49

Limits and Limit Laws in Calculus

Sum Law for 0:06:53

Sum Law for Limits of Complex Functions Revisited

(Single-Variable Calculus 1) 0:02:58

(Single-Variable Calculus 1) Proof of Sum Rule

Epsilon Delta of 0:08:19

Epsilon Delta of Sum Law

Cal limit of 0:00:17

Cal limit of sums = sum of limits proof delta epsilon

Limits in Calculus 0:19:53

Limits in Calculus -- Limit Sum Law Proof

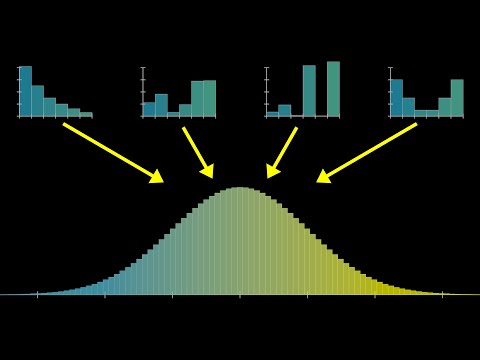
But what is 0:31:15

But what is the Central Limit Theorem?

THEOREM PROOF: LIMIT 0:18:40

THEOREM PROOF: LIMIT LAW FOR SUM OF CONVERGENT SEQUENCE | CONCEPTUAL VIEW| SEQUENCE | URDU.

How to Find 0:13:18

How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example

Комментарии
Автор

Hello, just wanna ask, in 5:03 how did you arrive at ε/2? Thanks :)

joshtumacay
Автор

Great videos! Suggestion - Maybe if you add a number prefix in the title of the video, it would make it easier to follow from one to another in an optimal sequence and also help categorize them in sub-topics.

christian.adriano
Автор

Excellent video! Other proofs for this concept online (and in my my notes) did not go into nearly as much detail behind the rationale for the steps👍

laith
Автор

Hey, great video! Are there videos for the multiplication and division like this one?

martin_skachkov
Автор

You have offered a really nice proof. Thank you so much!

jingyiwang
visit shbcf.ru