T-Test vs Z-Test #maths #statistics #datascience #machinelearning #stats

In this video, we talk about when we should use a t-test and when we should use a z-test.

*Follow Me*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

*Channel Support*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
The best way to support the channel is to share the content. ;)

If you'd like to also support the channel financially, donating the price of a coffee is always warmly welcomed! (completely optional and voluntary)
► Bitcoin (BTC): 3C6Pkzyb5CjAUYrJxmpCaaNPVRgRVxxyTq
► Ethereum (ETH): 0x9Ac4eB94386C3e02b96599C05B7a8C71773c9281
► Cardano (ADA): addr1v95rfxlslfzkvd8sr3exkh7st4qmgj4ywf5zcaxgqgdyunsj5juw5
► Tether (USDT): 0xeC261d9b2EE4B6997a6a424067af165BAA4afE1a

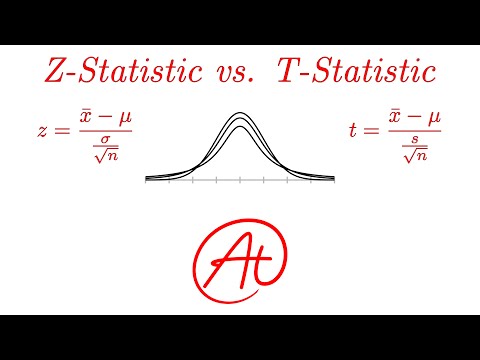
#ztest #ttest #studenttest #statistics #datascience #machinelearningIn this video, we talk about the z-test, a statistical method used to determine whether there is a significant difference between sample data and a population mean. We also discuss how it differs from the t-test, focusing on when to use each test based on sample size and whether the population standard deviation is known.

*References*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

*Related Videos*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

*Contents*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
00:00 - Intro
00:31 - Z-Test
00:55 - T-Test
01:35 - Sample size
02:03 - Z-Test Types
02:47 - Z-Table
03:16 - Outro

*Follow Me*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

*Channel Support*
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
The best way to support the channel is to share the content. ;)

If you'd like to also support the channel financially, donating the price of a coffee is always warmly welcomed! (completely optional and voluntary)
► Bitcoin (BTC): 3C6Pkzyb5CjAUYrJxmpCaaNPVRgRVxxyTq
► Ethereum (ETH): 0x9Ac4eB94386C3e02b96599C05B7a8C71773c9281
► Cardano (ADA): addr1v95rfxlslfzkvd8sr3exkh7st4qmgj4ywf5zcaxgqgdyunsj5juw5
► Tether (USDT): 0xeC261d9b2EE4B6997a6a424067af165BAA4afE1a

[runsurfswim]

Thank you for contributing to learn-scrolling

[et]

Thanks for this! very useful for revision when preparing for a test or interview.

[gonzalodiaz]

I just decided to trust in central limit theorem 😅

[hammey]

Just to clarify: Never use a t-test when testing for proportions. **for proportions** you first ask if both:
1) n*p_0 > 10 and n*(1-p_0) > 10
if yes, then use a z-test for proportions
if no, then you could use appropriate non-parametric test.

when testing a mean or difference of means (i.e. one vs two sample), only then do we ask ourselves "do we know the population standard deviation(s)?" use z-test if we do and t-test if we do not. However both z-test and t-test for means require either n>= 30 or population(s) to be normally distributed (the n>= 30 is just an arbitrarily large enough sample size that ensures the sample mean of an i.i.d. random sample of any distribution is normally distributed by central limit theorem); a necessary condition for both tests to function correctly. Thus, similarly to proportions if n>=30 and normally distributed population are both violated, then we will usually resort to some sort of appropriate non-parametric test.

as a final remark: for two sample t-test (testing the difference of means between two samples and assuming either n1 + n1 >= 30 or we know both samples are independent and normally distributed) we don't know the true standard deviations of each population. However if we have reason to assume that they should have the same standard deviation, then we should use a **pooled** two sample t-test.


here is a link to a nice dichotomous key chart:

[cristian-bull]

With unkown std, If your sample is greater than 30, it means that you "can" use z-test and you'll probably be fine, not that you "should" becase it's better.

[.marcelluschristian]

How can we not know about population's standard deviation? If we have tge data, can't we just calculate the Stdev first?

Please enlighten me, i'm a beginner at statistics

[bb-jrbn]

Great video!

just minor comments:

First. We never know the true standard deviation in real life. Just never. We can only estimate it. So we are forced to always use the estimated sd in real life.

Second, two crucial points are the assumption about the population distribution and the number of observations.

Hence, we have 4 cases (in all cases we use the estimated sd!):
A. small n, normal population distribution —> only t-test is ok
B. small n, unknown population distribution —> no valid test
C. big n, unknown or non-normal population distribution —> z-test is ok, t-test is also possible but less precise (here is the popular case for proportion test)
D. big n, normal population distribution —> t-test is ok, z-test is also possible but less precise

[joshstat]

In the end, we'll use t test since we can't collect all of people's height from a 1M populated city and make a generalization.

[Vishnu_naik-]

For small sample
n< 30
Use t- test

For large sample
n>= 30
Use z- test

Both are some subjects topics
Difference of mean like etc....

[efrainolivares]

Question about your graph: You colored `z-test` in RED, `t-test` in blue, do they correspond to the `red` and `blue` curves in the graph? I keep looking at the blue curve as associated with t-test, but it's NOT right?

[Marryatau]

With long tails in populations that describe nonlinear patterns it’s best to just get larger sample sizes and sigma could be more accurate, why not just use them both

[nubel]

What do you mean you don't know the sd. Can't you just like calculate it?
If it is something that can easily be calculated why does that ever need to be a junction in the decision making process.

[naeness]

In what cases do we even know the population's std

[MrJ]

Pretty sure for small samples you use non parametric tests

[eslamossama]

t-test it's best if sample size > 30 t-test = z-test

[daymenpollet]

Never use regular t test if ur observations are less than 30. This would require more nuanced methodes.

[HiddenTactics-]

Please, make your pronunciation clear. I appreciate the way you explained, but pronunciation is a barrier.