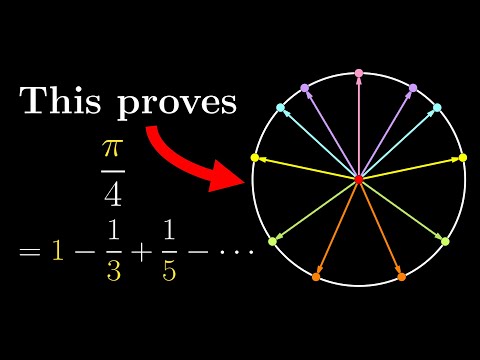
The simplest reason why π/4 = 1 - 1/3 + 1/5 -...

π/4 = 1 - 1/3 + 1/5 -..., also called the Leibniz series, is quite famous, but the usual proof involves differentiation or integration. The more visual geometric proof still relies a lot on some advanced theorems from number theory, but given how simple the series is, is it possible to have an even simpler proof? Yes! And this video tries to explain this.

Actually, similar to the previous proof, this proof has been at the video ideas list for quite a long time - so it's good to finally see this out!

By the way, on second thought, this looks similar to Fourier coefficients, at least the time average bit - though I can't see whether this is the same proof as the one using Fourier series of sgn(x). It feels very connected, but also very different in the sense that we don't need to use the Cesàro sums of the Fourier series. Please let me know if you have any ideas regarding this.

Video chapters:
00:00 Intro
00:45 Chapter 1: The setup
03:16 Chapter 2: The main argument
14:55 Chapter 3: Making this rigorous
17:33 Sponsored segment

This video was sponsored by Brilliant.

Sources (in order of appearance in the video):

A little more reading:

(Worth noting that this requires a bit more than just plugging in x = 1 in arctangent series - this requires the justification from Abel’s theorem)

(4) If you want to prove the Cesàro sum of the positions to be 0 more rigorously, here is the justification:
and

Music:
Asher Fulero - Beseeched
Aakash Gandhi - Heavenly, Kiss the Sky, Lifting Dreams
(From YouTube audio library)

Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:

If you want to know more interesting Mathematics, stay tuned for the next video!

SUBSCRIBE and see you in the next video!

If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!

Social media:

For my contact email, check my About page on a PC.

See you next time!

[mathemaniac]

At the end, essentially during the argument, both sides of the sum are just Cesàro sums, just that the LHS can be interpreted as a regular sum, and so we proved the identity. For an even more rigorous treatment, read the description.

By the way, on second thought, this looks similar to Fourier coefficients, at least the time average bit - though I can't see whether this is the same proof as the one using Fourier series of sgn(x). It feels very connected, but also very different in the sense that we don't need to use the Cesàro sums of the Fourier series. Please let me know if you have any ideas regarding this.

[strikeemblem]

Regarding the missing link to the Fourier series of sgn(x), here is the connection:
.
At the very heart of the argument, you have constructed a function f(x) that is the same as the square wave, as it has the same fourier coefficients. In particular, this construction is for f(1), because of the setup used on the radius, and the "minute hand", see 10:50.
.
Jordan's criterion tells us that the square wave (which is of bounded variation), has its Fourier series S_N f(1) converging to 1/2(f(1+) + f(1-)). This is 0 by definition of the square wave. This should be compared with the RHS of the eqn in 14:45.
.
So why is it no coincidence that the method of Cesaro summation also gives us 0? The keyword is "good kernels". In the proof of Jordan's criterion, we will find the use of something called a "Dirichlet kernel" D_N(t). While this a kernel, it is not a "good" kernel. But we may use it to define the "Fejer kernel" F_N(t) = 1/n sum_k D_k (t), which is a "good kernel".
.
The Fejer kernel is closely related to Cesaro summation: If we consider the Cesaro summation of successive Fourier series, i.e. consider [cesaro f_n](x) = 1/n (S_0 f(x) + ... + S_N-1 f(x)), then this equals the convolution of the Fejer kernel with f at x, i.e. (F_N * f)(x) !!!
.
The precise result that connects everything is this: The Fejer kernel is a family of "good kernels". As a consequence we have, if f is L1(torus) + bdd + the limits f(x-) and f(x+) exist, then (F_N * f)(x) -> 1/2(f(x+) + f(x-)).
.
For our case x=1, this says that [cesaro f_n] (1) -> 1/2(f(1+) + f(1-)) = 0.

[archibaldhaddock]

Brilliant idea.
You are so underrated.
I request to bring more series or courses just like before, this will make us like you more.

[johnchessant]

Great video! By the same method averaging from 0:20 to 0:40, I found that 1 - 1/2 + 1/4 - 1/5 + 1/7 - 1/8 + 1/10 - 1/11 + ... = pi/(3*sqrt(3)). Try doing that with calculus!

[yinq]

Great proof as always!
3:05 The average position is the center of gravity of the highlighted semi-circle.

[johnchessant]

(This definitely isn't rigorous, but) you can use geometric series to say that ... + exp(-2ix) + exp(-ix) + 1 + exp(ix) + exp(2ix) + ... = 1/(1-exp(ix)) + 1/(1-exp(-ix)) - 1, which indeed simplifies to 0. In fact, you can even put z = exp(ix) and get that the sum over all integer powers of z is 0. With z = 2, this leads to the whole 1 + 2 + 4 + 8 + ... = -1 business which leads us to 2-adics...

[thelosttomato]

My favorite way to prove this is by using the expansion for ln(1+x)
ln(1+x)= x- x^2/2+x^3/3-x^4/4....
plugging in ix instead of x, we get
ln(1+ix)= ix +x^2/2-ix^3/3-x^4/4.... etc
separating out the real and imaginary parts, we get,
inf) + (x^2/2-x^4/4 + x^6/6... inf)
plugging in x=1, we notice that the imaginary part on the right is our desired sum, call it S
ln(1+i)= S*i + (x^2/2-x^4/4 + x^6/6... inf)
ln(1+i) can be written as ln(sqrt(2)*e^(ipi/4))= 1/2 ln(2)+i*pi/4
equating imaginary parts, we get S=pi/4
It's one of the coolest things I've ever done in math, and it just randomly clicked when I was sitting in class lol

[ajreukgjdi]

Me: mom, can we get calculus
Mom: we have calculus at home
The calculus at home: "you have to be careful when adding up infinitely many things"

This just feels like calculus with more steps. It's just that your dx (or rather dt) steps are of size 1/2 hour. The only step you're missing is to let dt approach zero and boom, calculus. You just don't add any resolution after 1/2 hour

[captainsnake]

It’s amazing how many beautiful “ah ha” moments there are in this proof. Finding d using the average velocity, finding the sum of all the tips with a rotation, etc. I loved it.

[iaroslavragel]

Very nice proof. But still it requires calculus. Even to rigorously define an average of something over a period of time one needs integration. So rigorously speaking this "proof" does not use calculus because it's not a proof, but only a sketch, an explanation. A roadmap for a rigorous proof, if you want. And when one starts making this proof rigorous he finds out he needs calculus. And this should not be a surprise because the statement of the problem itself is already made in terms of calculus. Infinite series summation is already calculus in essence.

[PASHKULI]

you lost me at 3:00 placing the yellow dot on a dashed line and not on the intersection of dashed with circle.

[Mutual_Information]

Just discovered this channel. Very impressed!

[Infinium]

Lovely visualised proof, thanks for sharing!

[chriszachtian]

Sorry, this time you lost me at 11:00...
But I will continue to keep up

[matrix]

Hi Trevor! I'm a high school student. I've a question which came in my mind a long time ago but I'm unable to solve it.

The problem is: Take N number of random points on the circumference of the circle. Join them to form a polygon. What's the probability that the polygon so formed contains the centre of the circle?

[caspermadlener]

This argument might be useful to proof Dirichlet's theorem (the one about primes in arithmetic progressions)!
This is not only an easy way to have moduli, but addition and multiplication and addition both work amazing!
Also, I wouldn't be surprised if this would result in the 69420th proof of quadratic reciprocity :)

[raulyazbeck]

Thank you for this video! Now watching

[victorribera]

I have to admit that the one from 3b1b is more apealing to me, but this one is really beautiful too, great job

[swamiaman]

Thumbs up if you don't understand anything even after watching the whole video 😂.

[dopplershift]

Dude, I love the style of your videos! Do you base it off of 3blue1brown's? Love your content!