filmov
tv
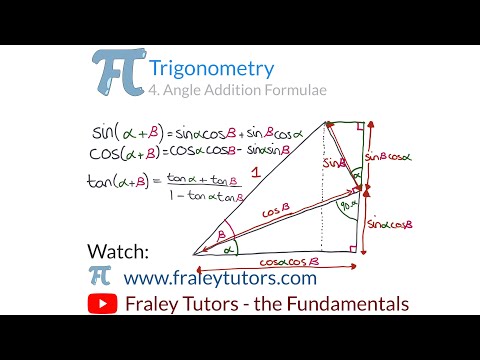
Proof of angle addition formula for cosine | Trigonometry | Khan Academy

Показать описание
Missed the previous lesson?
Trigonometry on Khan Academy: Big, fancy word, right? Don't be fooled. Looking at the prefix, tri-, you could probably assume that trigonometry ("trig" as it's sometimes called) has something to do with triangles. You would be right! Trig is the study of the properties of triangles. Why is it important? It's used in measuring precise distances, particularly in industries like satellite systems and sciences like astronomy. It's not only space, however. Trig is present in architecture and music, too. Now you may wonder...how is knowing the measurement and properties of triangles relevant to music?? THAT is a great question. Maybe you'll learn the answer from us in these tutorials!
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Trigonometry channel:
Комментарии
 0:08:26
0:08:26
 0:06:02
0:06:02
 0:08:47
0:08:47
 0:01:59
0:01:59
 0:02:07
0:02:07
 0:13:16
0:13:16
 0:04:21
0:04:21
 0:04:15
0:04:15
 0:10:19
0:10:19
 0:07:35
0:07:35
 0:07:45
0:07:45
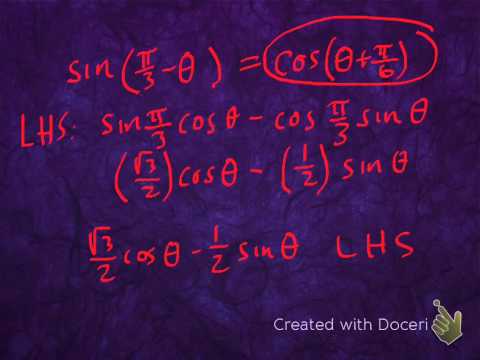 0:04:18
0:04:18
 0:13:19
0:13:19
 0:03:06
0:03:06
 0:02:01
0:02:01
 0:03:40
0:03:40
 0:07:44
0:07:44
 0:07:37
0:07:37
 0:04:01
0:04:01
 0:12:30
0:12:30
 0:14:39
0:14:39
 0:04:36
0:04:36
 0:05:27
0:05:27
 0:02:04
0:02:04