filmov
tv
Negative half factorial

Показать описание
In this video, I computed negative half factorial using the shifted gamma function.
Negative half factorial
Why is Pi here? | Half factorial without Gamma function #SoME3
what is half factorial? (1/2)!=? via. Gamma function
Generalized negative half factorial
What Is The Factorial Of 1/2? SURPRISING (1/2)! = (√π)/2
Can we have negative factorial?
How to Take the Factorial of Any Number
Minus half factorial??? Yes, let's calculate this thing.
How do I find the factorial of a negative number?
One Half Factorial ? (1/2)!
Feynman integration example 38 - Negative 1/2 Factorial
The Secret Behind -1 Factorial
Negative Factorial | (-1/2) Factorial
Factorial of Negative One Half is the Square Root of PI
FACTORIAL OF NEGATIVE HALF | FACTORIAL OF -1/2 | Proof | Amresh Harsh Academy | #iitjee
Negative Factorial Discovered | Universal Numbers (New)
factorial of negative fraction #shorts
why 0!=1 in 30 Seconds. (Shortest 0 factorial proof) #shorts
Half Factorial proof using the Gamma Function - (-1/2)!=sqrt(pi)
Multiply 2 Digit Numbers In 3 Seconds
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
What is the factorial of -½?
Factorials Explained!
When mathematicians get bored (ep1)
Комментарии
 0:08:59
0:08:59
 0:13:14
0:13:14
 0:10:53
0:10:53
 0:08:08
0:08:08
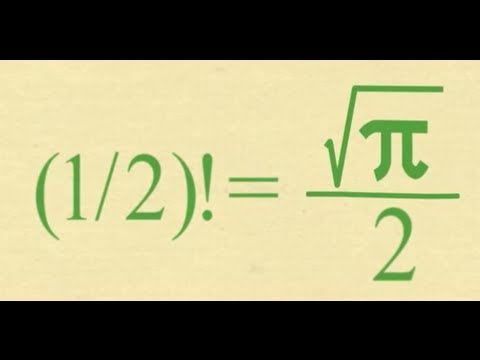 0:04:55
0:04:55
 0:19:44
0:19:44
 0:26:31
0:26:31
 0:05:52
0:05:52
 0:00:16
0:00:16
 0:04:21
0:04:21
 0:14:02
0:14:02
 0:05:03
0:05:03
 0:11:54
0:11:54
 0:16:49
0:16:49
 0:01:54
0:01:54
 0:06:07
0:06:07
 0:00:43
0:00:43
 0:00:30
0:00:30
 0:23:36
0:23:36
 0:00:08
0:00:08
 0:00:15
0:00:15
 0:12:46
0:12:46
 0:11:17
0:11:17
 0:00:37
0:00:37