filmov
tv
what is half factorial? (1/2)!=? via. Gamma function

Показать описание
What Is Half Factorial = ?
what is half factorial? (1/2)!=? via. Gamma function
What Is The Factorial Of 1/2? SURPRISING (1/2)! = (√π)/2
One Half Factorial ? (1/2)!
Why is Pi here? | Half factorial without Gamma function #SoME3
What is the factorial of -½?
(-1/2)! = ?
Fractional Factorial Design (DoE) Simply explained
1/2 Factorial, YES, Half Factorial
DOE Basics: Fractional Factorial Designs
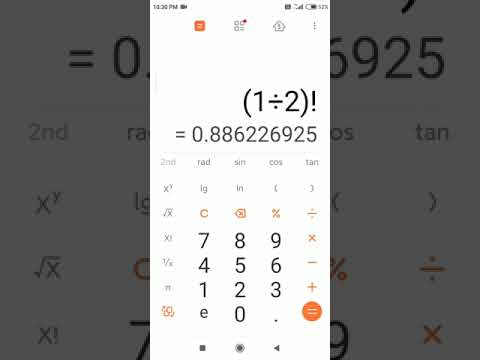
What is 1/2 factorial?
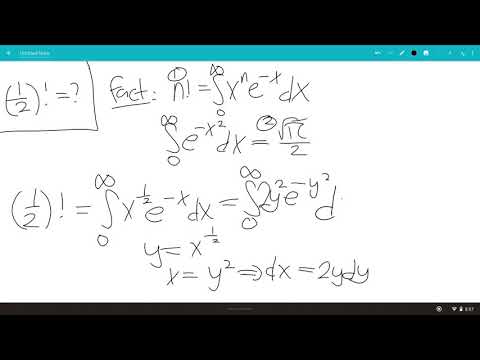
Half Factorial proof using the Gamma Function - (-1/2)!=sqrt(pi)
Find the value of 1/2 factorial
6÷2(1+2)=???
What is the factorial of 1/2
How to Take the Factorial of Any Number
Half factorial using the gamma function
When mathematicians get bored (ep1)
what is the factorial of 1/2?surprising (1/2)!=(√pi)/2 #mathsvideotech #iitjee
(1/2)! : Finding the value of (1/2)! । Factorial Function । Mathematics । The Social Pi
What is 1/2 factorial? - Gamma Function
How REAL Men Integrate Functions
Introduction to Basic One-Half Fractional Factorial 2k Design of Experiments DOE Details Explained
5 simple unsolvable equations
Why 0! = 1 ? | Why 0 factorial is equal to 1? #shorts
Комментарии
 0:10:53
0:10:53
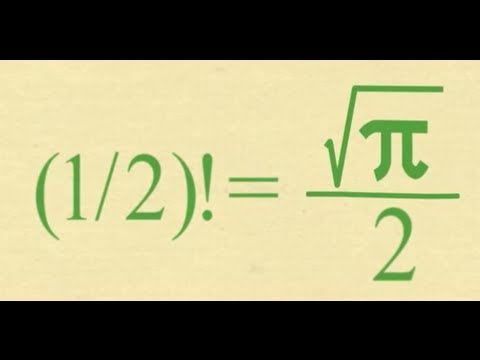 0:04:55
0:04:55
 0:04:21
0:04:21
 0:13:14
0:13:14
 0:12:46
0:12:46
 0:01:13
0:01:13
 0:12:54
0:12:54
 0:01:59
0:01:59
 0:01:00
0:01:00
 0:03:00
0:03:00
 0:23:36
0:23:36
 0:02:50
0:02:50
 0:01:21
0:01:21
 0:02:14
0:02:14
 0:26:31
0:26:31
 0:15:21
0:15:21
 0:00:37
0:00:37
 0:00:51
0:00:51
 0:07:35
0:07:35
 0:19:01
0:19:01
 0:00:35
0:00:35
 0:08:16
0:08:16
 0:00:50
0:00:50
 0:01:00
0:01:00