filmov
tv
Abstract Algebra, Lec 4A: Group Definition, Basic Properties of Groups, Cayley Tables, Observations

Показать описание
Abstract Algebra Course, Lecture 4A.
(0:00) Super Bowl comments.
(0:35) Have a clicker for powerpoint and will use overhead projector today.
(1:06) Lecture summary.
(1:35) Definition of a group: binary operation (closure), associativity, existence of identity, existence of inverses.
(8:06) Prove that the identity element is unique.
(13:24) Prove the left cancellation law.
(20:38) Cayley tables for Z3 and Z4.
(27:45) Introduction to the idea of a subgroup (like a subspace of a vector space from Linear Algebra).
(29:37) Review U(n) (the group of units modulo n, under multiplication mod n).
(31:02) Make Cayley tables for U(8) and U(10).
(38:31) Observation that U(8) and U(10) are not isomorphic.
Bill Kinney, Bethel University mathematics department
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Abstract Algebra, Lec 4A: Group Definition, Basic Properties of Groups, Cayley Tables, Observations
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Example of Subgroups and Proper Subgroups
Cycle Notation of Permutations - Abstract Algebra
Universal Algebra and Lattice Theory - Lecture 1: Introduction and background
LINEAR ALGEBRA Lec 4a (COMPLETE SOLUTIONS) || MA Eco Entrance 2023 ||#DSE #isi #jnu #igidr #iitjam
Abstract Algebra, Lec 18B: Normal Subgroups, Factor Groups (a.k.a. Quotient Groups)
Abstract Algebra, Lec 3B: Modular Arithmetic on Equivalence Classes, Number Theory Proofs
Introduction to Abstract Algebra
Abstract Algebra Lecture 7: Cayley Tables
Group Theory 4a: 2x2 matrices integer valued with unit determinant
AKPotW: Alternating Group Generators [Group Theory]
A non-abelian group all of whose subgroups are normal (Example of a Hamiltonian group)
Functions IIT Questions NO 11 ( X Class)
Modern Algebra - 4 || Symmetric or Permutation Group ||
Coding Theory and Linear Algebra
Example of Group: GL(2,R) (2 of 3)
Matrix Lie Groups: Lecture 1 part 1: complex and quaternions
Group Theory 4b: nxn matrices nonzero determinant
1.4 Basic Properties of Groups
Making Subgroup Lattices is Fun! (Construct Subgroup Lattice for Cyclic Group ℤ20)
Alternating Group -- Abstract Algebra Examples 12
Comment yes for more body language videos! #selfhelp #personaldevelopment #selfimprovement
Group Theory in Physics 1-A: Abstract Algebra & Reality (in Persian)
Комментарии
 0:39:51
0:39:51
 0:00:15
0:00:15
 0:02:50
0:02:50
 0:12:37
0:12:37
 0:40:46
0:40:46
 1:17:14
1:17:14
 0:27:31
0:27:31
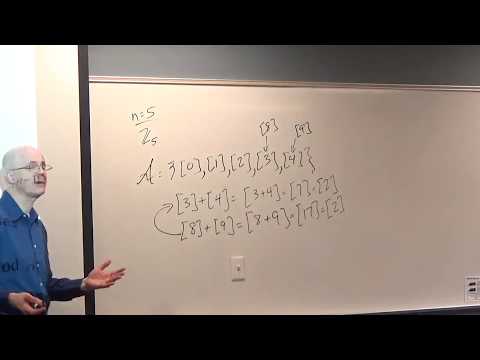 0:30:09
0:30:09
 0:23:01
0:23:01
 1:07:38
1:07:38
 0:09:25
0:09:25
 0:03:39
0:03:39
 0:03:53
0:03:53
 0:00:48
0:00:48
 0:27:32
0:27:32
 0:12:31
0:12:31
 0:08:25
0:08:25
 0:59:51
0:59:51
 0:03:01
0:03:01
 0:18:16
0:18:16
 0:10:35
0:10:35
 0:10:07
0:10:07
 0:00:22
0:00:22
 0:56:39
0:56:39