filmov
tv
Abstract Algebra, Lec 18B: Normal Subgroups, Factor Groups (a.k.a. Quotient Groups)
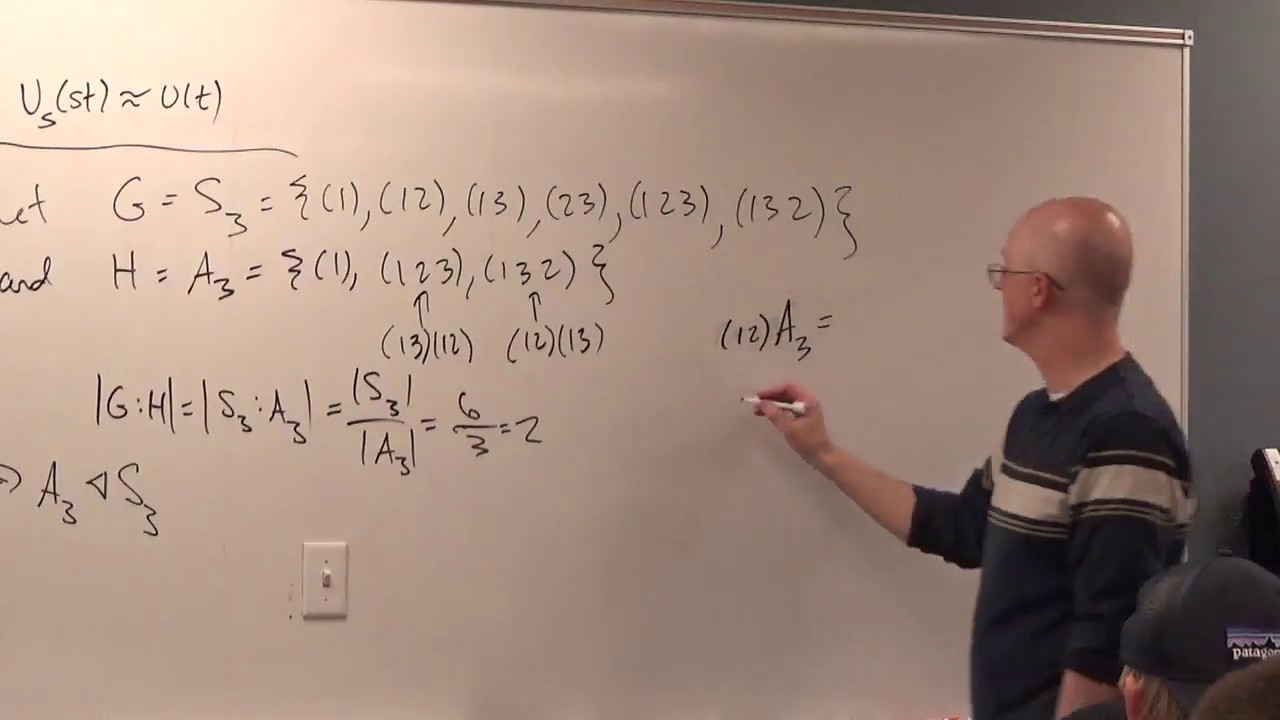
Показать описание
(0:00) Mention typo from previous slide.
(0:45) Example of a normal subgroup: H = A3 is normal in G = S3.
(7:09) The normal subgroup test and an example: outline of proof that {(1), (12)(34), (13)(24), (14)(23)} is normal in A4.
(14:54) Comment about when HK is a subgroup of G.
(15:32) Definition of a factor (quotient) group, both as a set, and with its binary operation of coset multiplication (aH)(bH) = abH (and in additive notation: (a + H) + (b + H) = (a + b) + H.
(19:15) Quickly mention that the group operation of coset multiplication must be shown to be well-defined.
(19:40) Example: Z/H, where H is the cyclic subgroup of Z generated by 3. This is isomorphic to Z3 (make Cayley table).
(25:53) The G/Z Theorem: If G/Z(G) is cyclic, then G is Abelian.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Abstract Algebra, Lec 18B: Normal Subgroups, Factor Groups (a.k.a. Quotient Groups)
Abstract Algebra, Lec 18A: External Direct Products Calculations & Isomorphisms, Normal Subgroup...
Abstract Algebra | Normal Subgroups
Abstract Algebra: normal subgroups and the Quotient Group, 9-24-18
Groups: A Normal Subgroup and Quotient Group of the Quaternions
Abstract Algebra 60: Quotient groups
Abstract Algebra. Quotient Groups 2
The normal subgroup property is not transitive
Abstract Algebra 1.4 : Kernels and Normal Subgroups
Groups: An Example of a Normal Subgroup and a Quotient Group
Abstract Algebra 1.3 : Subgroups, Normal Subgroups, and the Quotient Group
NORMAL SUBGROUP DEFINITION -ABSTRACT ALGEBRA
Abstract Algebra. Quotient Groups 1
Group Theory 40, Normal Subgroups and Factor groups, examples
Abstract Algebra 9.3: Factor Groups
Abstract Algebra Lectures Part 1: Groups, Definitions and Examples
Quotient Groups
Normal subgroups and quotient groups
Abstract Algebra: normal subgroup proofs, normal subgroups Dn, 10-3-27
Quotient group 2 - example: S₃
Abstract Algebra 9.2: Normal Subgroup Test
Groups: Subgroups of S_3
Kernel of a Homomorphism of Groups: Homomorphism and Isomorphism of groups: Part 2
Abelian Group | Normal Subgroup | Discrete Mathematics | MDU
Комментарии
 0:27:31
0:27:31
 0:34:35
0:34:35
 0:06:10
0:06:10
 0:52:12
0:52:12
 0:05:00
0:05:00
 0:08:28
0:08:28
 0:21:37
0:21:37
 0:03:15
0:03:15
 0:11:34
0:11:34
 0:06:01
0:06:01
 0:12:04
0:12:04
 0:03:32
0:03:32
 0:23:42
0:23:42
 0:14:46
0:14:46
 0:09:35
0:09:35
 0:23:05
0:23:05
 0:20:35
0:20:35
 0:14:53
0:14:53
 0:52:17
0:52:17
 0:01:07
0:01:07
 0:06:50
0:06:50
 0:06:39
0:06:39
 0:23:26
0:23:26
 0:08:25
0:08:25