filmov
tv
Abstract Algebra, Lec 3B: Modular Arithmetic on Equivalence Classes, Number Theory Proofs

Показать описание
(0:00) Another example of modular arithmetic on equivalence (congruence) classes (this time mod 5). It's isomorphic to Z5 (cyclic group of order 5).
(2:52) Review division algorithm and notion of what it means for one number to divide another.
(5:07) Review primes, composites, Fundamental Theorem of Arithmetic.
(6:59) Second (Strong) Principle of Mathematical Induction to prove the existence portion of the Fundamental Theorem of Arithmetic.
(17:07) Animation of Sieve of Eratosthenes for finding primes.
(19:29) There are infinitely many primes and the idea of its (most beautiful) proof by contradiction.
(23:09) Prove Euclid's Lemma based on the fact that the greatest common divisor (gcd) of two integers is a linear combination of the integers (and therefore two relatively prime (coprime) integers have a linear combination that equals the unity 1).
Bill Kinney, Bethel University mathematics department
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Abstract Algebra, Lec 3B: Modular Arithmetic on Equivalence Classes, Number Theory Proofs
Abstract Algebra | 8. Modular Arithmetic
Abstract Algebra: modular arithmetic
WHAT IS MODULAR ARITHMETIC? | ABSTRACT ALGEBRA
Abstract Algebra Course, Lecture 1: Introduction to Groups, Modular Arithmetic, Sets, & Function...
Abstract Algebra II: basic module theory, 3-18-22 part 1
Abstract Algebra, Lec 4A: Group Definition, Basic Properties of Groups, Cayley Tables, Observations
Modular Equivalence
G is not group under addition modulo 3
Logical Reasoning???#viral #vidumzn
Abstract Algebra | Introduction to Unique Factorization Domains
Calculus 1, Lecture 3B: Exponential Functions Fundamental Properties (also see the end of Lec 3A)
MATH0005 L12b: equivalence classes
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
congruent classes
Number Theory | Congruence and Equivalence Classes
Abstract Algebra, Lec 3A: Defining Inverse Functions, Review Group Examples & Equivalence Relati...
14-1. Multiplication Method: Proof
Construct Fields of Order 5^2 = 25 and 3^3 = 27 (Prime Power Order) as Factor Rings of ℤp[x]
COC4010_1.19_Crypto Maths3 _Galois Fields_Modular Polynomial Arithmetic
Addition and Multiplication modulo | Group Theory
Abstract Algebra: irred implies prime in PID, how to find inverse in poly factor ring, 11-2-18 p2
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
Henri Darmon: Andrew Wiles' marvelous proof
Комментарии
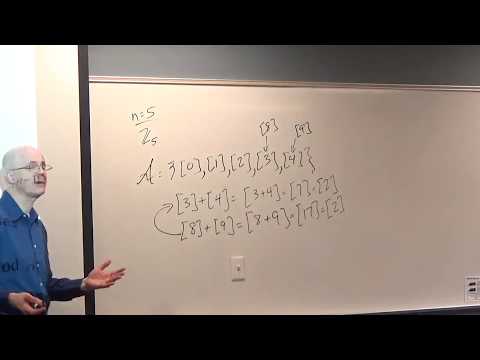 0:30:09
0:30:09
 0:17:03
0:17:03
 0:54:42
0:54:42
 0:07:26
0:07:26
 1:07:40
1:07:40
 0:59:51
0:59:51
 0:39:51
0:39:51
 0:03:27
0:03:27
 0:05:19
0:05:19
 0:00:11
0:00:11
 0:11:08
0:11:08
 0:31:43
0:31:43
 0:07:44
0:07:44
 0:00:12
0:00:12
 0:20:17
0:20:17
 0:09:50
0:09:50
 0:36:41
0:36:41
 0:04:50
0:04:50
 0:20:32
0:20:32
 0:24:11
0:24:11
 0:11:07
0:11:07
 0:07:11
0:07:11
 0:00:13
0:00:13
 0:54:26
0:54:26