filmov
tv
If the equation x^2+2x + 3 = 0 and ax^2+bx+c = 0 , a,b,c ∈ R, have a comman root , then a b: c is

Показать описание
If the equation x^2+2x + 3 = 0 and ax^2+bx+c = 0 , a,b,c ∈ R, have a comman root , then a b: c is
(a)1:2:3
(b) 3:2:1
(c) 1:3:2
(d) 3 : 1 : 2
quadratic equation, Impetus gurukul
#quadratic_equation
@Impetus Gurukul
--
To buy complete Course please Visit–
join Impetus Gurukul live classes via the official Website:
--
Algebra Playlist:
Permutations & Combinations:
Matrices:
Determinants:
Binomial Theorem:
Progression ( A.P,G.P, H.P & Special Series):
Quadratic equation & Inequations:
Set & Relations:
Complex Number:
--
Our Social links
---
Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where
a, b, c are real numbers, a 0.
In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree
2, is a quadratic equation. But when we write the terms of p(x) in descending order of
their degrees, then we get the standard form of the equation. That is, ax2 + bx + c = 0,
a 0 is called the standard form of a quadratic equation.
In general, a real number is called a root of the quadratic equation
ax2 + bx + c = 0, a 0 if a 2 + b+ c = 0. We also say that x = is a solution of
the quadratic equation, or that satisfies the quadratic equation. Note that the
zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic
equation ax2 + bx + c = 0 are the same.
Quadratic Formula = [-b ± √(b² - 4ac)]/2a
Important Quadratic Equation Formulas
The following list of important formulas is helpful to solve quadratic equations.
• The standard form of a quadratic equation is ax2 + bx + c = 0
• The discriminant of the quadratic equation is D = b2 - 4ac
• For D ‘Greater than’ 0 the roots are real and distinct.
• For D = 0 the roots are real and equal.
• For D ‘Less than’ 0 the roots do not exist, or the roots are imaginary.
• The formula to find the roots of the quadratic equation is x = −b±√b2−4ac2a−b±b2−4ac2a.
• The sum of the roots of a quadratic equation is α + β = -b/a = - Coefficient of x/ Coefficient of x2.
• The product of the Root of the quadratic equation is αβ = c/a = Constant term/ Coefficient of x2
• The quadratic equation having roots α, β, is x2 - (α + β)x + αβ = 0.
• The condition for the quadratic equations a1x2+b1x+c1=0a1x2+b1x+c1=0, and a2x2+b2x+c2=0a2x2+b2x+c2=0 having the same roots is (a1b2−a2b1)(b1c2−b2c1)(a1b2−a2b1)(b1c2−b2c1) = (a2c1−a1c2)2(a2c1−a1c2)2.
• For positive values of a (a ‘Greater than’ 0), the quadratic expression f(x) = ax2 + bx + c has a minimum value at x = -b/2a.
• For negative value of a (a ‘Less than’ 0), the quadratic expression f(x) = ax2 + bx + c has a maximum value at x = -b/2a.
• For a ‘Greater than’ 0, the range of the quadratic equation ax2 + bx + c = 0 is [b2 - 4ac/4a, ∞)
• For a ‘Less than’ 0, the range of the quadratic equation ax2 + bx + c = 0 is : (∞, -(b2 - 4ac)/4a]
---
+quadratic equation,Impetus gurukul,Relationship Between Coefficients and Roots of Quadratic Equation,Quadratic Equation solutions,JEE previous year's question's solution,Quadratic Equation - Formulas,Tricks for Solving Quadratic equation,solve quadratic equation,Quadratic equation roots formula,Sum and product of roots of quadratic equation,nda quadratic equation,NIMCET quadratic equation,jee quadratic equation
(a)1:2:3
(b) 3:2:1
(c) 1:3:2
(d) 3 : 1 : 2
quadratic equation, Impetus gurukul
#quadratic_equation
@Impetus Gurukul
--
To buy complete Course please Visit–
join Impetus Gurukul live classes via the official Website:
--
Algebra Playlist:
Permutations & Combinations:
Matrices:
Determinants:
Binomial Theorem:
Progression ( A.P,G.P, H.P & Special Series):
Quadratic equation & Inequations:
Set & Relations:
Complex Number:
--
Our Social links
---
Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where
a, b, c are real numbers, a 0.
In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree
2, is a quadratic equation. But when we write the terms of p(x) in descending order of
their degrees, then we get the standard form of the equation. That is, ax2 + bx + c = 0,
a 0 is called the standard form of a quadratic equation.
In general, a real number is called a root of the quadratic equation
ax2 + bx + c = 0, a 0 if a 2 + b+ c = 0. We also say that x = is a solution of
the quadratic equation, or that satisfies the quadratic equation. Note that the
zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic
equation ax2 + bx + c = 0 are the same.
Quadratic Formula = [-b ± √(b² - 4ac)]/2a
Important Quadratic Equation Formulas
The following list of important formulas is helpful to solve quadratic equations.
• The standard form of a quadratic equation is ax2 + bx + c = 0
• The discriminant of the quadratic equation is D = b2 - 4ac
• For D ‘Greater than’ 0 the roots are real and distinct.
• For D = 0 the roots are real and equal.
• For D ‘Less than’ 0 the roots do not exist, or the roots are imaginary.
• The formula to find the roots of the quadratic equation is x = −b±√b2−4ac2a−b±b2−4ac2a.
• The sum of the roots of a quadratic equation is α + β = -b/a = - Coefficient of x/ Coefficient of x2.
• The product of the Root of the quadratic equation is αβ = c/a = Constant term/ Coefficient of x2
• The quadratic equation having roots α, β, is x2 - (α + β)x + αβ = 0.
• The condition for the quadratic equations a1x2+b1x+c1=0a1x2+b1x+c1=0, and a2x2+b2x+c2=0a2x2+b2x+c2=0 having the same roots is (a1b2−a2b1)(b1c2−b2c1)(a1b2−a2b1)(b1c2−b2c1) = (a2c1−a1c2)2(a2c1−a1c2)2.
• For positive values of a (a ‘Greater than’ 0), the quadratic expression f(x) = ax2 + bx + c has a minimum value at x = -b/2a.
• For negative value of a (a ‘Less than’ 0), the quadratic expression f(x) = ax2 + bx + c has a maximum value at x = -b/2a.
• For a ‘Greater than’ 0, the range of the quadratic equation ax2 + bx + c = 0 is [b2 - 4ac/4a, ∞)
• For a ‘Less than’ 0, the range of the quadratic equation ax2 + bx + c = 0 is : (∞, -(b2 - 4ac)/4a]
---
+quadratic equation,Impetus gurukul,Relationship Between Coefficients and Roots of Quadratic Equation,Quadratic Equation solutions,JEE previous year's question's solution,Quadratic Equation - Formulas,Tricks for Solving Quadratic equation,solve quadratic equation,Quadratic equation roots formula,Sum and product of roots of quadratic equation,nda quadratic equation,NIMCET quadratic equation,jee quadratic equation
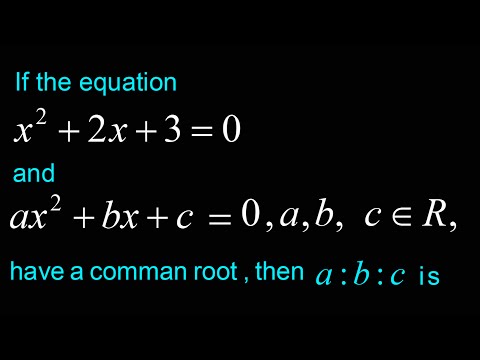 0:00:27
0:00:27
 0:02:12
0:02:12
 0:01:55
0:01:55
 0:02:15
0:02:15
 0:02:19
0:02:19
 0:02:17
0:02:17
 0:01:17
0:01:17
 0:02:00
0:02:00
 0:02:53
0:02:53
 0:10:34
0:10:34
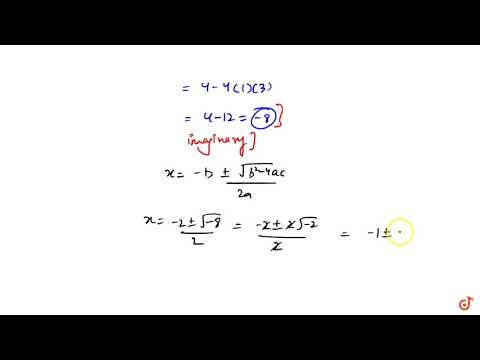 0:03:02
0:03:02
 0:12:29
0:12:29
 0:03:15
0:03:15
 0:02:43
0:02:43
 0:01:47
0:01:47
 0:02:36
0:02:36
 0:03:23
0:03:23
 0:02:21
0:02:21
 0:02:53
0:02:53
 0:03:19
0:03:19
 0:03:47
0:03:47
 0:05:51
0:05:51
 0:00:57
0:00:57
 0:02:03
0:02:03