filmov
tv
Limit of x*sin(1/x) as x approaches infinity || Two Solutions

Показать описание
Limit of x*sin(1/x) as x approaches infinity || Two Solutions
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Limit of x*sin(1/x) as x approaches 0 | Calculus 1 Exercises
Limit of x*sin(1/x) as x approaches Infinity | Calculus 1 Exercises
Discover the Limit of x*sin(1/x) as x Approaches Infinity | Unraveling Calculus Mysteries 🧠📈🚀...
lim xsin(1/x) as x goes to 0
Limit of sin(1/x) as x approaches 0 Does Not Exist | Calculus 1 Exercises
Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises
Limit of xsin(1/x) as x approaches infinity vrs limit of xsin(1/x) as x approaches 0
Limit of x*sin(1/x^2) as x approaches 0 (Squeeze Theorem) | Calculus 1 Exercises
GATE 2025: Data Science & AI - Calculus & Optimization Practice + PYQs (Part 2) | GfG GATE
30 Limit Approaching Infinity for Trigonometric Function xsin(1/x)
Limit of (1-x)sin(1/(1-x)) as x approaches 1 | Calculus 1 Exercises
Limit of x sin(1/x) as x approaches infinity
Limit x sin(1/x) as x goes to infinity ll Limit of cos(1/x) as x tend to 0
Limit of (cos1/x+sin1/x)^x as x approaches infinity
Limit for Trigonometric Functions sin(1/x) as x approaches zero
Limit of x*sin(1/x) as x approaches infinity || Two Solutions
the most controversial limit in calculus 1
Limit of sin(1/x) as x approaches to zero | What is the limit of sin (1/x)?
Oscillating Discontinuity - sin(1/x)
Limits of Trigonometric Functions
CALCUL DE LIMITE XSIN (1/X) QUAND X TEND VERS 0
The limit of sin(1/x) as x approaches 0 does not exist (Proof) [ILIEKMATHPHYSICS]
Proofs: Lim sinx/x =1 and lim [cosx -1] /x =0 as x goes to zero from geometry
limit x tend to 0 sin 1/x
Комментарии
 0:08:14
0:08:14
 0:09:23
0:09:23
 0:03:58
0:03:58
 0:15:35
0:15:35
 0:04:36
0:04:36
 0:03:59
0:03:59
 0:06:29
0:06:29
 0:04:24
0:04:24
 0:49:53
0:49:53
 0:02:24
0:02:24
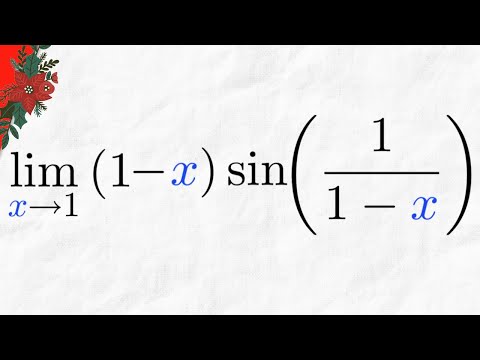 0:12:03
0:12:03
 0:01:38
0:01:38
 0:04:17
0:04:17
 0:03:48
0:03:48
 0:10:12
0:10:12
 0:03:46
0:03:46
 0:08:19
0:08:19
 0:11:50
0:11:50
 0:03:20
0:03:20
 0:15:23
0:15:23
 0:01:28
0:01:28
 0:08:46
0:08:46
 0:17:08
0:17:08
 0:02:44
0:02:44