filmov
tv
Pre-Calculus Prep: Evaluating the Cosecant of an Inverse Secant [csc(sec^-1(-sqrt(6)/2))]

Показать описание
To evaluate the cosecant of an inverse secant, csc(sec^(-1)(-√6/2)), you can follow these steps:
1. Start with the given expression: csc(sec^(-1)(-√6/2)).
2. Use the definition of the inverse secant function: sec^(-1)(x) represents the angle whose secant is x.
3. Evaluate the inverse secant: In this case, sec^(-1)(-√6/2) represents the angle whose secant is -√6/2.
4. Determine the angle: To find the angle whose secant is -√6/2, you need to identify the quadrant where the secant value is negative and the reference angle within that quadrant.
5. Analyze the secant value: Since -√6/2 is negative, the angle lies in either the second or third quadrant, where the secant is negative.
6. Find the reference angle: The reference angle is the acute angle formed between the positive x-axis and the terminal side of the angle in standard position. In this case, the reference angle is π/6 (30 degrees) because the secant of π/6 is 2/√3, which simplifies to √6/3.
7. Determine the angle: To find the angle whose secant is -√6/2, you need to consider the quadrants where the secant is negative. In the second quadrant, the angle whose secant is √6/2 is π - π/6, which simplifies to (6π - π)/6 = 5π/6 (or 150 degrees). In the third quadrant, the angle is π + π/6, which simplifies to (6π + π)/6 = 7π/6 (or 210 degrees).
8. Evaluate the cosecant: The cosecant (csc) of an angle is the reciprocal of the sine. Since the sine of an angle is the reciprocal of the cosecant, csc(θ) = 1/sin(θ).
9. Determine the sine of the angle: The sine of the angle can be found using the reference angle and the quadrant where the angle lies. In this case, since the angle lies in the second quadrant, the sine value is positive. The sine of 5π/6 (150 degrees) is 1/2.
10. Evaluate the cosecant: Now that we have the sine value, we can find the cosecant of the angle. csc(5π/6) = 1/(1/2) = 2.
Therefore, csc(sec^(-1)(-√6/2)) = 2.
By evaluating the inverse trigonometric functions and working with reciprocal relationships, you can find the value of trigonometric expressions. Understanding inverse trigonometric functions and reciprocal relationships is crucial in pre-calculus for solving trigonometric equations, working with angles, and analyzing various trigonometric phenomena.
These videos are designed to review and reteach Precalculus and Collegeboard Pre-CALC AP content. My videos cover functions, polynomials, exponential and logarithmic expressions, trigonometry, parametric equations, polar coordinates, vectors, matrices and systems, conic sections, discrete mathematics, sequences and series; and an introduction to calculus.
Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa .
.
.
#math #maths #mathskills #mathsucks #mathstudent #mathsmemes #mathstudents #mathsteacher #mathsisfun #gcsemaths #quickmaths #mathstutor #mathsclass #mathstricks #mathsjokes #brunomathsson #mathstations #mathslover #mathsproblems #mathsfun #alevelmaths #earlymaths #mathsquiz #mathsmeme #mathsmock #mathsnotes #mathsbeauty #ilovemaths #lovemaths #addmaths #mathsforlife #mathsweek #mathsgames #mathsexam #eyfsmaths #mathsrevision #primarymaths #ihatemaths #mathslesson #mathstuition
 0:03:38
0:03:38
 0:16:41
0:16:41
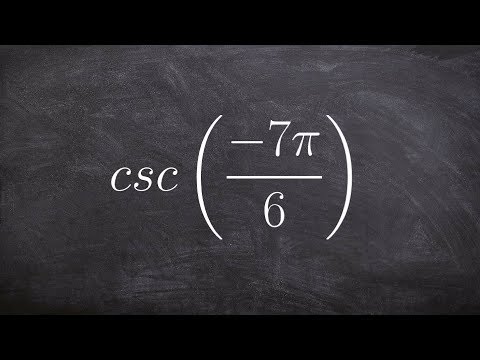 0:02:43
0:02:43
 0:13:06
0:13:06
 0:00:43
0:00:43
 0:42:12
0:42:12
 0:01:30
0:01:30
 0:21:52
0:21:52
 0:04:00
0:04:00
 0:02:09
0:02:09
 0:26:36
0:26:36
 0:19:57
0:19:57
 0:10:59
0:10:59
 0:16:45
0:16:45
 0:22:47
0:22:47
 0:00:59
0:00:59
 0:00:29
0:00:29
 0:30:27
0:30:27
 0:05:02
0:05:02
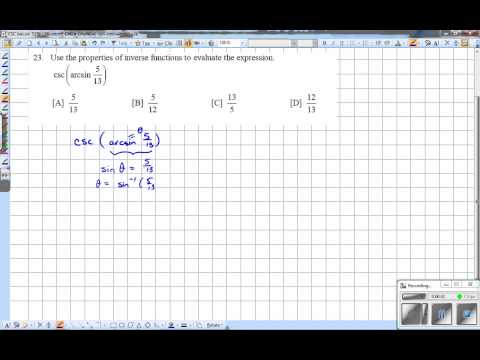 0:01:38
0:01:38
 0:56:24
0:56:24
 0:26:01
0:26:01
 0:22:37
0:22:37
 0:43:01
0:43:01