filmov
tv
Find The Height 'h' In This Shape | Learn Two Easy Methods

Показать описание
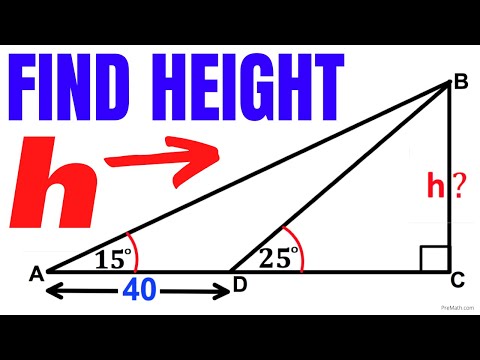
Find the height h in the right triangle | Important Geometry and Trigonometry skills explained
Calculate the height h | Important Geometry and Algebra skills explained
Calculate the height h | Important Geometry and Algebra skills explained
Think outside the Box | Find the height h in a triangle | Important Geometry skills are explained
Math Olympiad | Find height h in the triangle | [Important Geometry skills explained] #math #maths
Angle of Elevation: Find the Height 'h' in this Right Triangle | Fast & Easy Tutorial
Find The Height 'h' In This Shape | Learn Two Easy Methods
Can you find the Height of This Shape? | Step-by-Step Tutorial
Solved GATE DA 2024 Question Paper | DETAILED VIDEO SOLUTIONS | DA & AI | Q. 52 Rooted Binary Tr...
Find the height h of the right triangle | Inscribed circle | Important Geometry skills explained
Can you find the Height of the Triangle in 60 Seconds? | Two Simple Methods
In the figure a stone is projected at a cliff of height
Height modeled by the quadratic equation. When does the object hit the ground.
Finding height of a parallelogram
Minimum height h of mirror to see the shoe
Trigonometry Word Problem, Finding The Height of a Building, Example 1
Word Problem: Height of projectile h(t)=-16t^2+64t. What time to reach 48 feet?
A block of mass m 2.0 kg is dropped from height h=40 cm onto a spring of spring constant k = 196
Use Calculus to find the volume of the cap of a sphere with height h and radius r.
KM DTS 33 Q5 A ball is released from a height h. If t, and t₂ be the time required to complete
How to find the height of a ball and time it takes using velocity
Maximum Height and Velocity h(t) = -5t^2 + 30t + 1 Derivative Application
Determine the force of this distribution and specify the height h
Height of a cuboid given volume
Комментарии
 0:06:22
0:06:22
 0:08:01
0:08:01
 0:05:57
0:05:57
 0:05:50
0:05:50
 0:08:08
0:08:08
 0:06:43
0:06:43
 0:08:21
0:08:21
 0:04:29
0:04:29
 0:02:52
0:02:52
 0:08:04
0:08:04
 0:06:12
0:06:12
 0:09:47
0:09:47
 0:02:32
0:02:32
 0:01:41
0:01:41
 0:01:45
0:01:45
 0:07:31
0:07:31
 0:03:37
0:03:37
 0:02:36
0:02:36
 0:03:12
0:03:12
 0:04:03
0:04:03
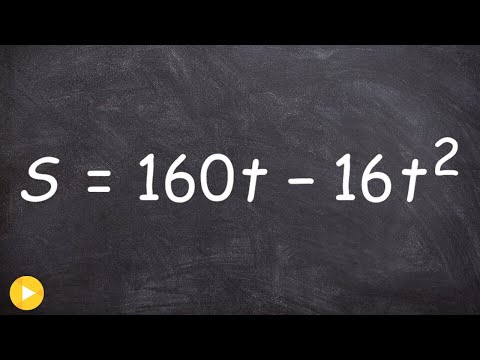 0:03:32
0:03:32
 0:05:56
0:05:56
 0:04:02
0:04:02
 0:02:22
0:02:22