filmov
tv
The Derivative as a Rate of Change

Показать описание
In calculus, a derivative is a fundamental concept that measures how a function changes as its input (independent variable) changes. It provides information about the rate of change of a function at a specific point.
Derivatives are used extensively in calculus to solve problems related to rates of change, optimization, and understanding the behavior of functions. They have applications in various fields, including physics, engineering, economics, and more, making them a crucial concept in mathematics.
Derivatives are used extensively in calculus to solve problems related to rates of change, optimization, and understanding the behavior of functions. They have applications in various fields, including physics, engineering, economics, and more, making them a crucial concept in mathematics.
Calculus - The derivative as a rate of change
Understanding Differentiation Part 2: Rates of Change
Interpretation of the Derivative as a Rate of Change
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
The paradox of the derivative | Chapter 2, Essence of calculus
Section 1.8 The Derivative as a Rate of Change
The Derivative as a Rate of Change
Related Rates in Calculus
Sketch the Derivative: Position, Velocity, and Acceleration
Introduction to Related Rates
Derivatives Explained in One Minute
Visual Derivative Definition!
Maths104 - 11.3 The derivative as a rate of change
Chapter 2.4 The Derivative as a Rate of Change
3.3 Derivative as rate of change
Related rates intro | Applications of derivatives | AP Calculus AB | Khan Academy
3.4: The Derivative as a Rate of Change
The Derivative As A Rate Of Change
Calc 1 - The Derivative as a Rate of Change
The Derivative as a Rate of Change (Calculus Problems and Solutions)
Derivatives... What? (NancyPi)
Example of derivative as limit of average rate of change
Definition of the Derivative
Derivative as a Rate
Комментарии
 0:04:09
0:04:09
 0:05:31
0:05:31
 0:08:08
0:08:08
 0:07:16
0:07:16
 0:16:50
0:16:50
 0:12:13
0:12:13
 0:00:56
0:00:56
 0:08:53
0:08:53
 0:08:14
0:08:14
 0:10:32
0:10:32
 0:01:30
0:01:30
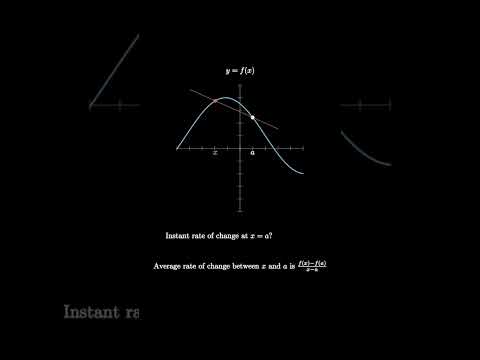 0:01:00
0:01:00
 0:18:47
0:18:47
 0:29:23
0:29:23
 0:06:18
0:06:18
 0:07:43
0:07:43
 0:31:11
0:31:11
 0:25:21
0:25:21
 0:48:52
0:48:52
 0:29:08
0:29:08
 0:14:30
0:14:30
 0:03:34
0:03:34
 0:23:31
0:23:31
 0:16:21
0:16:21