Solving the 1-D Heat/Diffusion PDE: Nonhomogenous Boundary Conditions

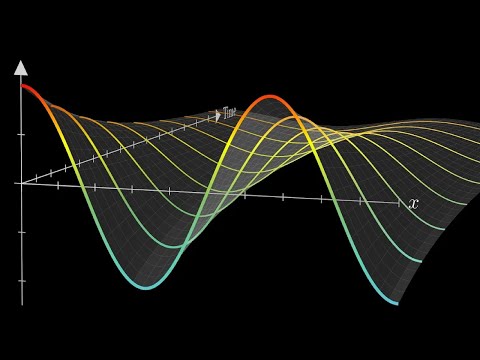
In this video, I solve the diffusion PDE but now it has nonhomogenous but constant boundary conditions. I show that in this situation, it's possible to split the PDE problem up into two sub-problems: one which gives a steady-state solution, and another which gives a transient solution.

I show that the transient solution obeys homogenous boundary conditions, and that using the steady state solution helps to remove the non-homogeneity. Solving the transient solution is just a simple matter of separating variables, in which case these two videos should help:

Questions? Ask in the comments!

[AG-pmtc]

my dude, just wanted to tell you, that your explanation has just the right amount of amount of theoretical background justification to make all of this stuff reasonable and not just bunch of steps from a "cookbook".
awesome stuff!

[fhzsduras]

I LOVE you! I wish you all the best in your academic and personal life. You deserve it for being such an angelic being!

[saapman]

Wow! The best PDE series ive seen so far! Great work.

[JORGEMARTINEZMARTIN-xdpe]

Thank you, I have a differential equations midterm in a couple of days and I just understood more about this problem with your 7 minutes video than in a couple hours of reading notes and solved exercises

[CarlosRamos-txer]

so clear; is very similar that a non-homogeneus ode, in this case your particular solution is the transient term and the homogeneus solucion would be the steady state, not exactly the same, but you can do an analogy

[achillesarmstrong]

this video is super cool. It explains non homogenour bc equation clearly.

[ozzyfromspace]

Thank you! I saw a solution to the heat equation where u(0, t) != u_0, and got so confused. It makes sense now that I’ve seen your explanation of how phi(x) settles to the boundary condition when given enough time. Again, many thanks!

[medhawinikapoor]

THANKYOU!1 exactly what i ws looking for!

[freeandreliablejeeprep]

thank you srila prabhupada, krishna and sir

[shandyverdyo]

I like ur videos and i want to ask something.

What i got is, So if we have inhomogeneous BC we can't use separation variables and must to change the BC into homogeneous then we be able to solve with the separation variable. Right?

Is there a way to solve the inhomogeneous BC of PDE without change it into homogeneous?

[Peter_]

I always use this method for all homogeneous separation-of-variables equations;
might as well do that since this method is a more general version anyway, and it also gives me lots of review practice.

[stavroschristodoulou]

What if the boundary conditions were:
a) Derivative at x=0 being some constant u_0
b) Derivative at x=L being some other constant u_L ??
Would there be steady state solutions? If yes, which ones?

[santiagosanz]

Hi! I don't understand why can't you use separation of variables with non homogeneus boundary conditions. Thank you.

[bandarubhavanishankar]

Could you please tell me how to solve heat equation for one boundary condition is constant temperature and other is variable. For example (two rods joined together in series)

[gelaarsde]

can you explain the greens functions.?

[remlatzargonix]

Would the integrals of the steady state solution have "constants" that a potential functions of t, since it is only the partial derivative wrt X that are zero?

[oyinebimie]

Hi Khan, Thank you so much for this video, it was totally helpful. I would like to ask what happens if the initial condition of the transient solution derived from the given formula turns out to be zero

[MrBogo]

HI ! I would like to solve a non homogenous Boundary conditions heat diffusion problem involving time dependent boundary conditions, so I have to solve transient heat equation with transient boundary conditon. This video let me believe that I can use this steady stade/transient state separation method to solve my problem, is it correct ? My second option is to use Laplace transform with transient condition however I can't find exemple to help me, have you got an idea about how do I have to procede ? Thks by advance.

Hugo

[fercho]

Great video! But I have one question: What happen if my B. Conditons are homogeneous, but my PDE, that is the same equation of this video, contains a constant, that i can call "a". In that case, my problem is nonhomogeneous, not by the B. Conditons but by the equation itself. Can i use this method of the sum of a steady and transient solutions?

[garcmodin]

Are you applying the Method of Eigenfunction Expansion in this video?