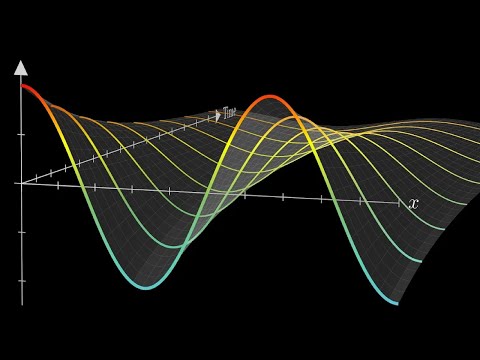
Solving the 1-D Heat/Diffusion PDE: General Nonhomogenous Boundary Conditions

preview_player
Показать описание
In this short video, I demonstrate how to solve a typical heat/diffusion equation that has general, time-dependent boundary conditions.

Questions? Let me know in the comments!

ERRATA: At 5:54, the boundary condition involving gamma and delta should be at x = L, not at x = 0.

  1. Faculty of Khan
  2. Physics
  3. Math
  4. Differential Equations
  5. PDEs
  6. Heat Equation
Рекомендации по теме
Solving the 1-D 0:11:09

Solving the 1-D Heat/Diffusion PDE by Separation of Variables (Part 1/2)

Solving the 1-D 0:07:25

Solving the 1-D Heat/Diffusion PDE: Nonhomogenous Boundary Conditions

Solving the 1-D 0:08:45

Solving the 1-D Heat/Diffusion PDE: Nonhomogenous PDE and Eigenfunction Expansions

Solving the 1-D 0:10:51

Solving the 1-D Heat/Diffusion PDE by Separation of Variables (Part 2/2)

Solving the 1-D 0:06:53

Solving the 1-D Heat/Diffusion PDE: General Nonhomogenous Boundary Conditions

Solving the heat 0:14:13

Solving the heat equation | DE3

Oxford Calculus: How 0:35:02

Oxford Calculus: How to Solve the Heat Equation

Solving the Heat 0:25:42

Solving the Heat Diffusion Equation (1D PDE) in Python

Introducing Parabolic PDEs 0:07:09

Introducing Parabolic PDEs (1-D Heat/Diffusion Eqn): Intuition and Maximum Principle

PDE: Heat Equation 0:21:17

PDE: Heat Equation - Separation of Variables

Solving the Heat 0:24:39

Solving the Heat Diffusion Equation (1D PDE) in Matlab

Session 4: Solution 0:32:46

Session 4: Solution to 1- dimensional heat (diffusion) equation with zero boundary conditions.

Solving The 1D 0:10:48

Solving The 1D & 2D Heat Equation Numerically in Python || FDM Simulation - Python Tutorial #4

Numerical Solution of 0:15:22

Numerical Solution of 1D Heat Conduction Equation Using Finite Difference Method(FDM)

Deriving the Heat 0:23:50

Deriving the Heat Equation: A Parabolic Partial Differential Equation for Heat Energy Conservation

Solving the Heat 0:11:28

Solving the Heat Equation with the Fourier Transform

Deriving finite difference 0:09:36

Deriving finite difference equation for 1D heat diffusion equation

Session 5: Solution 0:14:13

Session 5: Solution to 1- dimensional heat(diffusion) equation when both ends are insulated.

ME565 Lecture 19: 0:42:33

ME565 Lecture 19: Fourier Transform to Solve PDEs: 1D Heat Equation on Infinite Domain

Derivation of the 0:31:57

Derivation of the Heat Equation

PETSc Tutorial: Implicit 0:26:31

PETSc Tutorial: Implicit 1D Heat Diffusion

Solve 1-D heat 0:12:35

Solve 1-D heat equation (PDE) using finite difference and Crank Nicolson method in SCILAB

Solve 1D Transient 0:16:48

Solve 1D Transient Heat Conduction Problem Using Finite Difference FTCS Method

Solution of One 0:28:52

Solution of One Dimensional Heat Equation | One Dimensional Heat Equation Solution |1D Heat Equation

Комментарии
Автор

I don't know if it is me that is mistaken, but in 5:54 shouldn't the second boundary condition ( the one with gamma and delta coefficients) be for x=L? Otherwise, great video as always! (By the way, are you considering on making a series about series itself? I would really be interested in one of those.)

penisofflife
Автор

So PDEs use undetermined coefficients to solve for non-homogeneous boundary conditions. What if x depends on t, then how would you solve this equation?

dominicellis
Автор

Do you always assume that the inhomogeneous component is quadratic?

majormaki
Автор

hi, can you help me with a heat diffusion equation which is homogeneous and transient with general boundary condition but u0 and uL are functions of x instead of time. if the solution is the same as you taught here??

zahraabdoli
Автор

would you please check the article:analytical solution for three-dimensional stresses in a short length FGM hollow cylinder!
actually is not the same as problem i am solving but it has general boundary conditions which are not equal to a function of time.

zahraabdoli