filmov
tv
Solving the Heat Diffusion Equation (1D PDE) in Python

Показать описание
Solving the heat equation | DE3
Oxford Calculus: How to Solve the Heat Equation
Solving the Heat/Diffusion equation - part 1
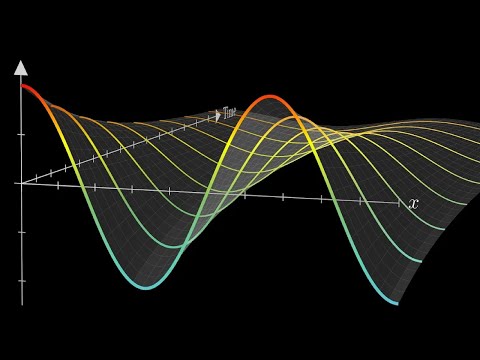
But what is a partial differential equation? | DE2
Solving the 1-D Heat/Diffusion PDE by Separation of Variables (Part 1/2)
Heat Equation
Session 4: Solution to 1- dimensional heat (diffusion) equation with zero boundary conditions.
Solving the Heat Diffusion Equation (1D PDE) in Python
Physics Adiabatic process 14 10 24 #Shorts #YouTube #Trending #Viral #News #Headlines
Understanding Conduction and the Heat Equation
Diffusion equation | Lecture 52 | Differential Equations for Engineers
Solving the 1-D Heat/Diffusion PDE: Nonhomogenous PDE and Eigenfunction Expansions
12.3: Heat Equation
Solving the Heat/Diffusion equation - part 3
Solving the Heat Diffusion Equation (1D PDE) in Matlab
Heat Transfer: Conduction Heat Diffusion Equation (3 of 26)
Solving the Heat Equation with the Fourier Transform
Heat Transfer - Chapter 2 - Example Problem 6 - Solving the Heat Equation in Cylindrical Coordinates
Solving PDEs with the Laplace Transform: The Heat Equation
Heat equation: Separation of variables
Heat Transfer L10 p1 - Solutions to 2D Heat Equation
Heat Transfer L14 p2 - Heat Equation Transient Solution
Heat Transfer - Chapter 2 - Derivation of the Heat Diffusion Equation
Heat Equation
Комментарии
 0:14:13
0:14:13
 0:35:02
0:35:02
 0:09:58
0:09:58
 0:17:39
0:17:39
 0:11:09
0:11:09
 0:10:48
0:10:48
 0:32:46
0:32:46
 0:25:42
0:25:42
 0:33:04
0:33:04
 0:18:21
0:18:21
 0:09:13
0:09:13
 0:08:45
0:08:45
 0:32:45
0:32:45
 0:08:48
0:08:48
 0:24:39
0:24:39
 0:57:29
0:57:29
 0:11:28
0:11:28
 0:20:04
0:20:04
 0:40:16
0:40:16
 0:47:14
0:47:14
 0:14:00
0:14:00
 0:11:51
0:11:51
 0:24:55
0:24:55
 0:21:19
0:21:19