Let the mean and standard deviation of marks of class A of 100 students | JEE Mains 2023 Statistics

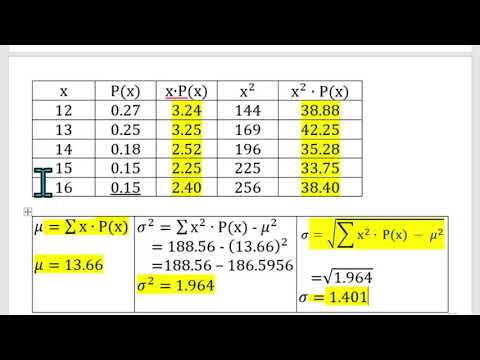
Let the mean and standard deviation of marks of class A of 100 students be respectively 40 , and the mean and standard deviation of marks of class B of n students be respectively 55 and 30 -α. If the mean and variance of the marks of the combined class of 100 + n students are respectively 50 and 350, then the sum of variances of classes A and B is

In this video, we solve an intriguing statistical problem involving the mean and variance of marks of two classes, A and B, with 100 and n students, respectively. We are given the mean and standard deviation of each class, and we need to determine the sum of their variances using the combined mean and variance of the two classes. This is a great problem to deepen your understanding of variance, mean, and how they relate in combined data sets!

Given Data:
Class A: 100 students, mean = 40, standard deviation = α
Class B: n students, mean = 55, standard deviation = 30 - α
Combined class: 100 + n students, mean = 50, variance = 350
Watch as we break down the steps and equations needed to find the sum of the variances of the two classes. Ideal for students preparing for exams and wanting to improve their understanding of statistics.