filmov
tv
8. Proving the Limit of a Composite Function

Показать описание
Here we essentially prove that a limit within a limit can exist in the same way that a function within a function can exist and this limit is important as it is the basis for proving other limits as well.
8. Proving the Limit of a Composite Function
proving the limit of a product is the product of the limits, epsilon-delta definition
Proof of a Limit Value Using Epsilon and Delta
Limit Laws - Proof of Sum Law
How to Write epsilon, delta-Proof for Limit of x^3 as x approaches -2
* PROOF 8: Uniqueness of the Limit Theorem (case of finite limits)
epsilon-N definition for a limit at infinity (introduction & how to write the proof)
how to easily write the epsilon-delta proofs for limits
From Zero to Hero: My Path as the Versatile Mage Who Masters All Magic! | Manhwa Recap
How To Tell If The Limit Exists
Proof 4.1: Unique Limit of a Sequence
The most important limit in Calculus // Geometric Proof & Applications
Example - Epsilon Delta Definition of Limit | L38 | Intro Complex @ranjankhatu
100 calculus limits (ft epsilon-delta definition and Riemann sum limits )
Prove that the limit of x^2 as x approaches 3 equals 9 using the epsilon-delta definition
Epsilon - Delta Proof (precise definition of the limit)
Limits of Trigonometric Functions
The Limit of a Sequence is Unique Proof
Proof: Limit Law for Quotient of Convergent Sequences | Real Analysis
Exponentials (Limit Example 8)
Squeeze Theorem
Why is pi here? And why is it squared? A geometric answer to the Basel problem
How To Find The Limit At Infinity
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Комментарии
 0:10:40
0:10:40
 0:28:27
0:28:27
 0:09:17
0:09:17
 0:08:18
0:08:18
 0:02:45
0:02:45
 0:12:56
0:12:56
 0:18:28
0:18:28
 0:08:28
0:08:28
 3:06:37
3:06:37
 0:09:22
0:09:22
 0:06:09
0:06:09
 0:11:54
0:11:54
 0:05:09
0:05:09
 7:29:13
7:29:13
 0:03:33
0:03:33
 0:20:11
0:20:11
 0:15:23
0:15:23
 0:05:14
0:05:14
 0:16:31
0:16:31
 0:08:21
0:08:21
 0:10:43
0:10:43
 0:17:08
0:17:08
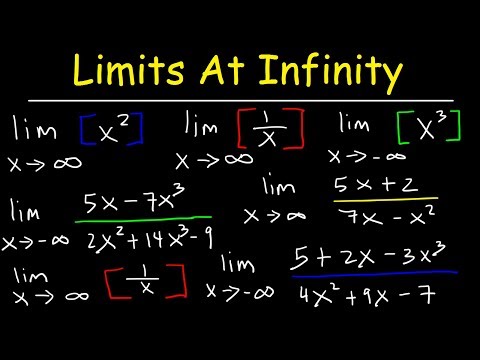 0:13:14
0:13:14
 0:18:27
0:18:27