filmov
tv
Proof: Limit Law for Quotient of Convergent Sequences | Real Analysis
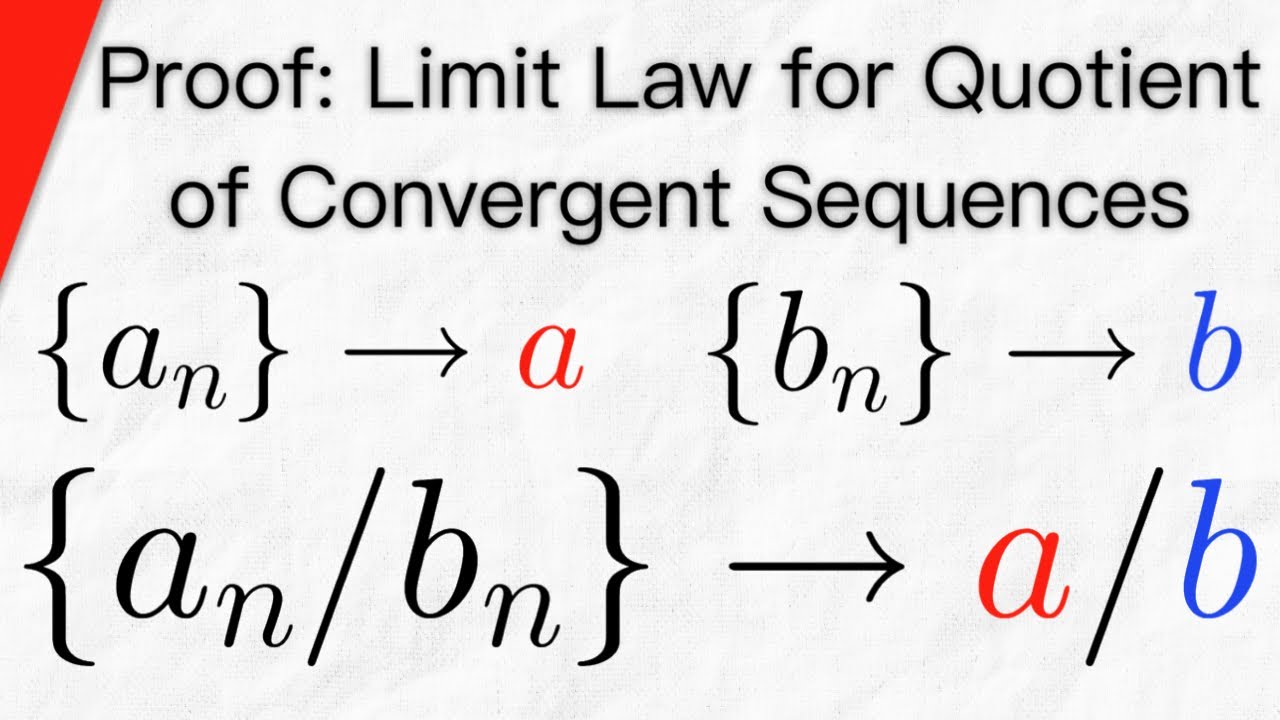
Показать описание
We prove the limit law for the quotient of convergent sequences. If a_n converges to a and b_n converges to b, then the sequence a_n/b_n converges to a/b, provided that b isn't 0, and each b_n is not 0. Put simply, the quotient of convergent sequences converges to the quotient of their limits. This is a slightly tricky proof using the epsilon definition of a convergent sequence, and some fun absolute value inequality manipulations!
★DONATE★
Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!
Follow Wrath of Math on...
★DONATE★
Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!
Follow Wrath of Math on...
Limit Laws - Proof of Quotient Law
Proof: Limit Law for Quotient of Convergent Sequences | Real Analysis
Delta Epsilon Proof of limit of a quotient of functions (General)
Proof of the Quotient Rule
The quotient rule for limits - formal proof
Theorem Proof: Limit law for the quotient of Convergent Sequences | Concept overview
Proof of Quotient Law, Constant Multiple Law and Difference Law (Limit Laws)
Reciprocals (Limit Example 7)
proving the limit of a product is the product of the limits, epsilon-delta definition
Limits in Calculus -- Limit Quotient Law Proof
Limit Laws - Proof of Product Law
Proving All the Sequence Limit Laws | Real Analysis
This is a very famous limit
Limit Laws - Proof of Sum Law
Product rule proof | Taking derivatives | Differential Calculus | Khan Academy
The Quotient Rule - Intuitive Proof
Quotient Rule Proof Using the Definition of a Derivative with Limits
Proof: Limit Law for Product of Convergent Sequences | Real Analysis
Prove of the Quotient Rule for Sequences
Proof: Limit Law for Sum of Convergent Sequences | Real Analysis
Limit law quotient
how to easily write the epsilon-delta proofs for limits
The Limit of Quotient of Two Functions ll Limit Rule ll My Dear Maths ll Dr Ganesh Kumar
Proof of the quotient rule
Комментарии
 0:14:37
0:14:37
 0:16:31
0:16:31
 0:12:50
0:12:50
 0:04:34
0:04:34
 0:07:56
0:07:56
 0:36:12
0:36:12
 0:08:19
0:08:19
 0:08:51
0:08:51
 0:28:27
0:28:27
 0:37:52
0:37:52
 0:12:52
0:12:52
 0:54:07
0:54:07
 0:00:48
0:00:48
 0:08:18
0:08:18
 0:09:25
0:09:25
 0:06:11
0:06:11
 0:18:53
0:18:53
 0:14:30
0:14:30
 0:14:37
0:14:37
 0:07:56
0:07:56
 0:25:41
0:25:41
 0:08:28
0:08:28
 0:19:06
0:19:06
 0:02:25
0:02:25