filmov
tv
Calculus with the Dirac Delta Function
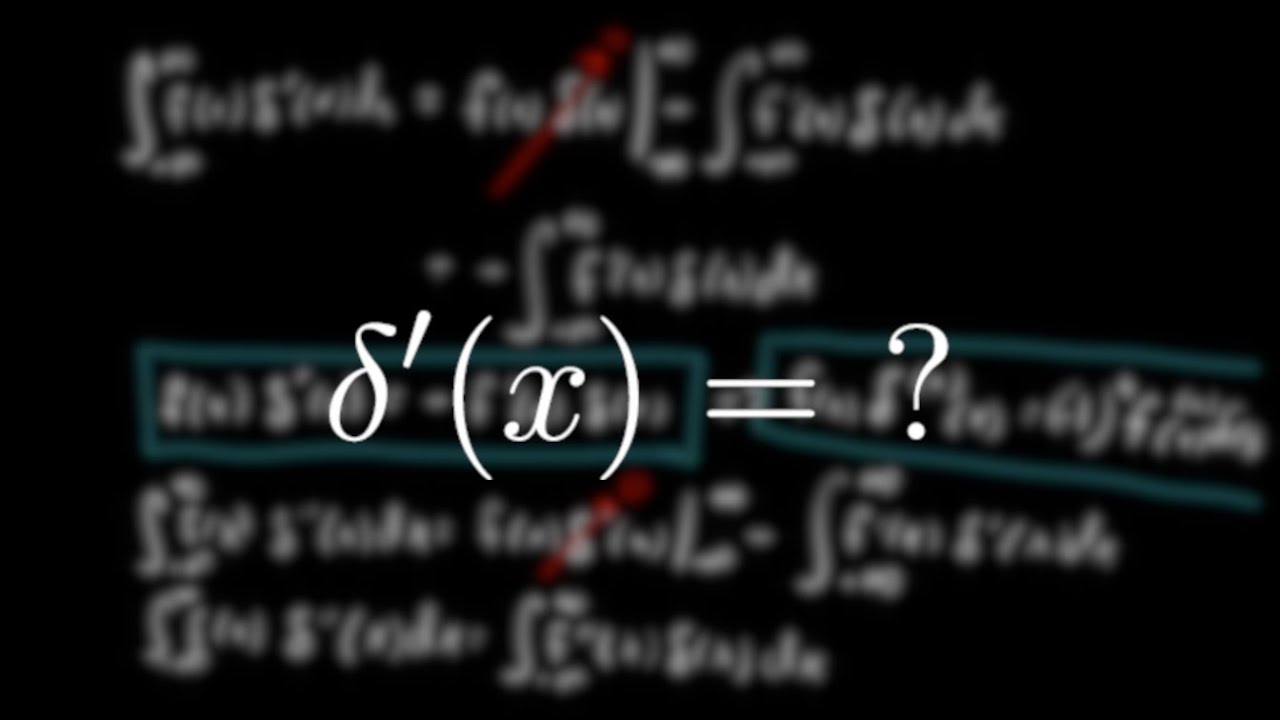
Показать описание
In this video I take a closer look at properties of the Dirac Delta Function involving integrals and derivatives.
For more videos in this series visit:
For more videos in this series visit:
The Dirac Delta 'Function': How to model an impulse or infinite spike
Calculus with the Dirac Delta Function
The Dirac Delta Function
Dirac Delta Derivative
Dirac's Delta Function
What is the Dirac Delta Function? An Intuitive Approach
Solving a DE with the Dirac Delta Function
Dirac delta function | Laplace transform | Differential Equations | Khan Academy
Dirac delta function | Lecture 33 | Differential Equations for Engineers
Proving A Property of the Derivative of the Dirac Delta Function
Dirac Delta Function
Dirac Delta as an approximation of Normal Distribution
Dirac Delta Function
Differential Equations: Lecture 13/21 - The Dirac Delta Function
Dirac delta function
Demystifying the Dirac Delta - #SoME2
Laplace of Dirac Delta function
Solving ODEs with Delta functions using Laplace Transforms
Dirac Delta
Laplace transform of the dirac delta function | Laplace transform | Khan Academy
9. What Exactly is the Dirac Delta Function? What is the Laplace Transform of the DDF?
Ch 5: What are Dirac deltas and wavefunction inner products? | Maths of Quantum Mechanics
Dirac Delta Function and Vector Calculus Theorems - University Physics
(Mathematical Methods of Physical) P3: Dirac Delta Function - BT 07 f
Комментарии
 0:09:25
0:09:25
 0:10:38
0:10:38
 0:07:14
0:07:14
 0:07:35
0:07:35
 0:09:10
0:09:10
 0:10:39
0:10:39
 0:03:20
0:03:20
 0:17:48
0:17:48
 0:12:31
0:12:31
 0:04:05
0:04:05
 0:03:15
0:03:15
 0:14:13
0:14:13
 0:05:17
0:05:17
 1:32:45
1:32:45
 0:07:43
0:07:43
 0:09:22
0:09:22
 0:01:51
0:01:51
 0:10:20
0:10:20
 0:23:17
0:23:17
 0:12:13
0:12:13
 0:11:23
0:11:23
 0:10:31
0:10:31
 0:50:51
0:50:51
 0:00:05
0:00:05