filmov
tv
The Fundamental Theorem of Line Integrals // Big Idea & Proof // Vector Calculus
Показать описание
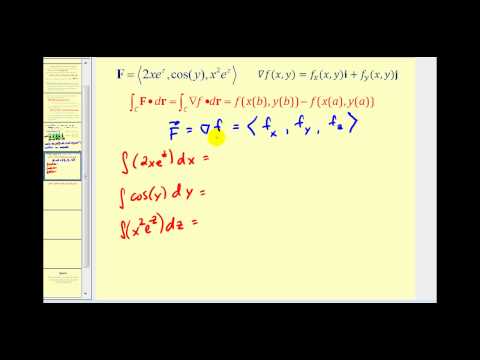
Back in 1st year calculus we have seen the Fundamental Theorem of Calculus II, which loosely said that integrating the derivative of a function just gave the difference of the function at the endpoints. That is, what happened in the middle did not matter. In this video we upgrade to the Fundamental Theorem of Line Integrals, which is a generalization of the Fundamental Theorem of Calculus. It says that when you take the line integral of a conservative vector field (ie one where the field can be written as the gradient of a scalar potential function), then this line integral is similarly just the difference of the function at the endpoints and is thus path independent - only the endpoints matter. In this video we will motivate this theorem, prove it formally, and connect the idea back to that of conservative vector fields.
0:00 FToC
1:24 Fundamental Thm of Line Integrals
2:50 Proof
5:33 Conservative Fields
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
0:00 FToC
1:24 Fundamental Thm of Line Integrals
2:50 Proof
5:33 Conservative Fields
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
0:06:38
The Fundamental Theorem of Line Integrals // Big Idea & Proof // Vector Calculus
0:04:16
The Fundamental Theorem for Line Integrals
0:09:15
The Fundamental Theorem of Line Integrals - Part 1
0:08:09
Fundamental Theorem for Line Integrals :: Conservative Vector Field Line Integral
0:14:21
Example of the Fundamental Theorem of Line Integrals
0:15:36
Fundamental Theorem of line integrals
0:15:27
Fundamental Theorem of Line Integrals
1:02:18
Calculus 3: The Fundamental Theorem for Line Integrals (Video #29) | Math with Professor V
0:03:19
What is vector calculus?
0:07:23
Solve the Line Integral with the Fundamental Theorem of Line Integrals - 16.3.14 Cengage
1:53:58
Line Integrals on CONSERVATIVE Vector Fields (Independence of Path): Calculus 3 Lecture 15.4
0:09:41
The Fundamental Theorem for Line Integrals
0:28:08
Calc 3 16.3 Notes: The Fundamental Theorem for Line Integrals
0:20:23
Multivariable Calculus 3.3.1 - The Fundamental Theorem of Line Integrals
0:12:07
Section 16.3: The Fundamental Theorem of Line Integrals
0:05:12
Fundamental theorem line integrals example
0:22:00
The Fundamental Theorem of Line Integrals
0:07:10
The Fundamental Theorem of Line Integrals - Part 2
0:14:03
Fundamental Theorem for Line Integrals
0:05:30
Multivariable calculus 4.2.2: Proof of the fundamental theorem of line integrals
0:09:19
Multivariable Calculus | Fundamental Theorem of Line Integrals
0:17:30
16.3 The Fundamental Theorem for Line Integrals
0:05:59
Multivariable Calculus: The Fundamental Theorem of Line Integrals - Introduction (16.3)
0:07:07
The Fundamental Theorem of Line Integrals
Комментарии