filmov
tv
What would make this equation true??
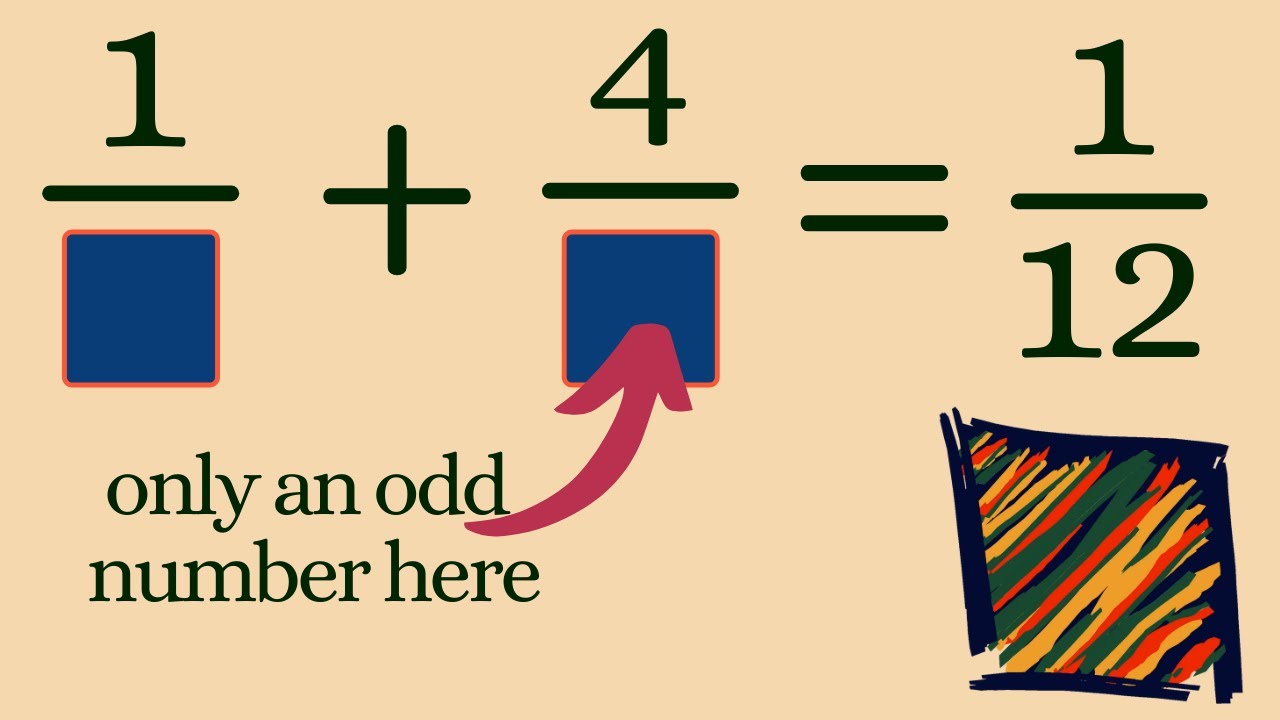
Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
What would make this equation true??
Can you solve this equation?
Solving an equation for y and x
Determine the values that make the equation true
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Solving an equation with variables on both side and one solution
Math Help : How to Write an Equation
Brain test make this equation correct
Solve an Equation with Square Roots #maths #math #solveequations #squareroot #matheducation #mathedu
Solving an equation for y and x using two steps
The Most Wholesome Math Equation
Chemical Equation Basics
Writing the equation from a graph
Linear Equation | Solving Linear Equations
Finding the Relation/Equation from a table
How do you solve a literal equation with all variables
Writing A Linear Equation From A Function Table
Make this equation true Brain Out
How To Find The Equation of a Line From a Graph | Algebra
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
Solving Linear Equation in One Variable #math #mathematics #equation #linearequations #mathtricks
Kepler’s Impossible Equation
Let’s Solve An Equation with Fractions….Step-by-Step….
Linear equation word problem | Linear equations | Algebra I | Khan Academy
Комментарии
 0:06:05
0:06:05
 0:00:28
0:00:28
 0:03:47
0:03:47
 0:02:08
0:02:08
 0:06:54
0:06:54
 0:02:36
0:02:36
 0:02:40
0:02:40
 0:00:35
0:00:35
 0:00:59
0:00:59
 0:03:12
0:03:12
 0:00:16
0:00:16
 0:03:35
0:03:35
 0:02:09
0:02:09
 0:11:20
0:11:20
 0:03:47
0:03:47
 0:01:59
0:01:59
 0:08:40
0:08:40
 0:00:46
0:00:46
 0:10:05
0:10:05
 0:00:30
0:00:30
 0:00:57
0:00:57
 0:22:42
0:22:42
 0:14:40
0:14:40
 0:05:59
0:05:59