filmov
tv
Markov Matrices

Показать описание
MIT 18.06SC Linear Algebra, Fall 2011
Instructor: David Shirokoff
A teaching assistant works through a problem on Markov matrices.
License: Creative Commons BY-NC-SA
Instructor: David Shirokoff
A teaching assistant works through a problem on Markov matrices.
License: Creative Commons BY-NC-SA
Markov Chains & Transition Matrices
Markov Matrices
Powers of Matrices and Markov Matrices
Markov Chains Clearly Explained! Part - 1
Markov chains with Matrices
The Transition Matrix
Steady-State Vectors for Markov Chains | Discrete Mathematics
Markoff Kette, Markov Kette, Übergangsprozess, stochastischer Prozess | Mathe by Daniel Jung
Markov Matrix Algebra
Transition Matrices & Markov Chains [IB Math AI HL]
Matrix Limits and Markov Chains
Prob & Stats - Markov Chains (8 of 38) What is a Stochastic Matrix?
Random walks in 2D and 3D are fundamentally different (Markov chains approach)
Intro to Linear Algebra - Markov Chains Example
Prob & Stats - Markov Chains (15 of 38) How to Find a Stable 3x3 Matrix
Introducing Markov Chains
Linear Algebra- Markov Chains and Stochastic Matrices
(Lecture 5) Markov Matrices
Intro to Markov Chains & Transition Diagrams
Markov Chains: n-step Transition Matrix | Part - 3
Prob & Stats - Markov Chains (9 of 38) What is a Regular Matrix?
Markov Chains - Part 7 - Absorbing Markov Chains and Absorbing States
Markov Chains - Part 9 - Limiting Matrices of Absorbing Markov Chains
Markov Chains and Transition Matrices
Комментарии
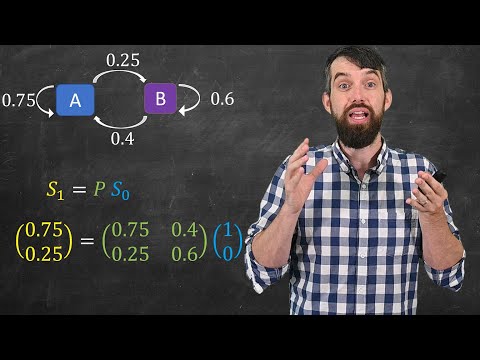 0:06:54
0:06:54
 0:11:49
0:11:49
 0:17:54
0:17:54
 0:09:24
0:09:24
 0:09:30
0:09:30
 0:13:03
0:13:03
 0:05:37
0:05:37
 0:04:23
0:04:23
 0:05:23
0:05:23
 0:10:19
0:10:19
 0:18:04
0:18:04
 0:03:50
0:03:50
 0:18:22
0:18:22
 0:10:00
0:10:00
 0:10:04
0:10:04
 0:04:46
0:04:46
 0:09:42
0:09:42
 0:52:46
0:52:46
 0:11:25
0:11:25
 0:08:34
0:08:34
 0:01:59
0:01:59
 0:12:05
0:12:05
 0:28:20
0:28:20
 0:10:59
0:10:59