Countable Sets, Uncountable Sets

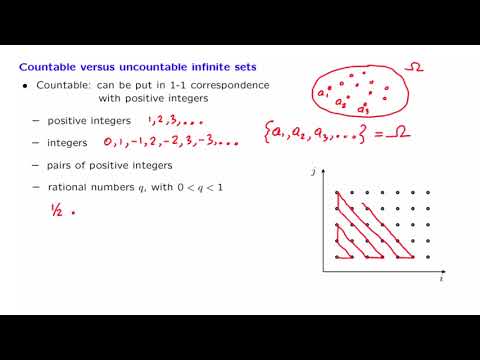
The cardinalities (numbers of elements) of the sets of natural numbers, integers, rational numbers, and real numbers are all infinite. Which one is "larger" or "smaller"? It turns out that the sets of natural numbers, integers, and rational numbers all have the "same" number of elements and are called countable, whereas the set of real numbers contains a far greater number of elements and is called uncountable. But how can we "count" infinities?