Find the maximum or minimum value of a quadratic equation using vertex form: real-world application

Find the maximum or minimum value of a quadratic equation using vertex form: real-world application

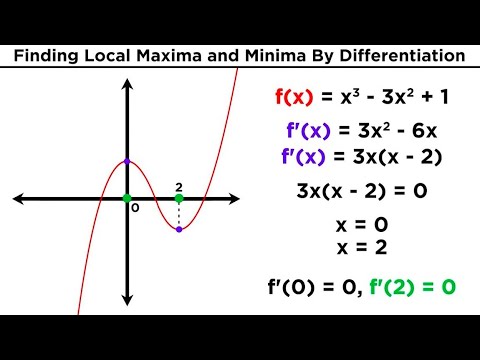
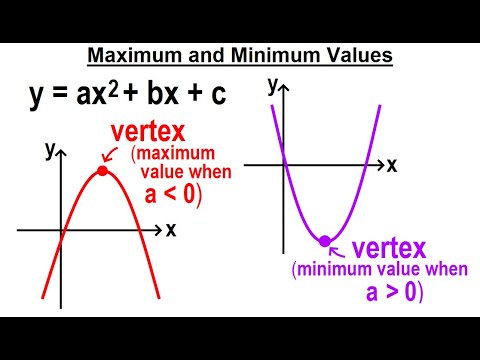
In this lesson you have learned how to find the maximum or minimum value of a real-world quadratic function by writing its equation in vertex form.

ADDITIONAL MATERIALS

STANDARDS

CCSS.HSA-SSE.B.3.b Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.

TEKS.A2.4.D transform a quadratic function 𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 to the form 𝑓(𝑥) = 𝑎(𝑥 - ℎ)² + 𝑘 to identify the different attributes of 𝑓(𝑥);

TEKS.A1.8.A solve quadratic equations having real solutions by factoring, taking square roots, completing the square, and applying the quadratic formula; and

IN.C.AD.4 Solve real-world and other mathematical problems finding local and absolute maximum and minimum points with and without technology.

IN.PC.QPR.1 Use the method of completing the square to transform any quadratic equation into an equation of the form (x – p)^2 = q that has the same solutions. Derive the quadratic formula from this form.

VA.F.AII.7.c extrema;