filmov
tv
Integral 1/(2+x^2) trig substitution. Let x=sqrt(2)*tan(theta) and use tangent secant identity.

Показать описание
Questions or requests? Post your comments below, and I will respond within 24 hours.
We compute the integral 1/(2+x^2) by applying trigonometric substitution. When we choose the trig substitution, we let x=sqrt(2)*tan(theta) so that when we square x, we can factor a 2 out of the denominator. We plan to use tangent secant identity, because we have the form "constant + variable squared" in the denominator.
After we make the 1/(2+x^2) trig substitution, we clean up the integral, guess the antiderivative, and substitute for theta in terms of x to obtain the final answer. We substitute for theta by solving the original substitution for theta, giving an inverse tangent of x/sqrt(2).
 0:09:36
0:09:36
 0:19:50
0:19:50
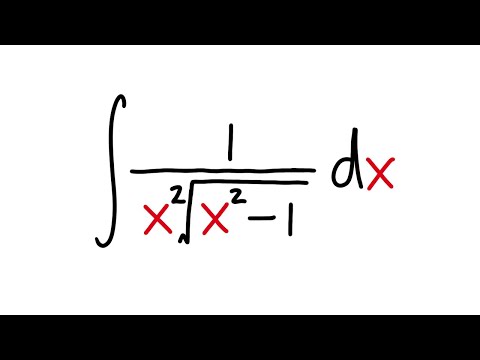 0:04:23
0:04:23
 0:08:01
0:08:01
 0:07:12
0:07:12
 0:15:55
0:15:55
 0:08:34
0:08:34
 0:07:19
0:07:19
 0:07:56
0:07:56
 0:25:15
0:25:15
 0:00:43
0:00:43
 0:02:42
0:02:42
 0:03:41
0:03:41
 0:06:47
0:06:47
 0:00:29
0:00:29
 0:01:01
0:01:01
 0:06:29
0:06:29
 0:07:40
0:07:40
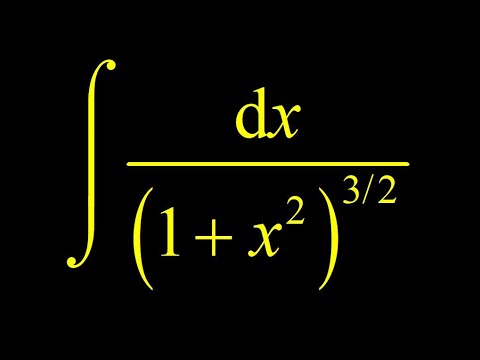 0:02:57
0:02:57
 0:06:45
0:06:45
 0:01:00
0:01:00
 0:04:31
0:04:31
 0:04:24
0:04:24