filmov
tv
Find angle in a semicircle.
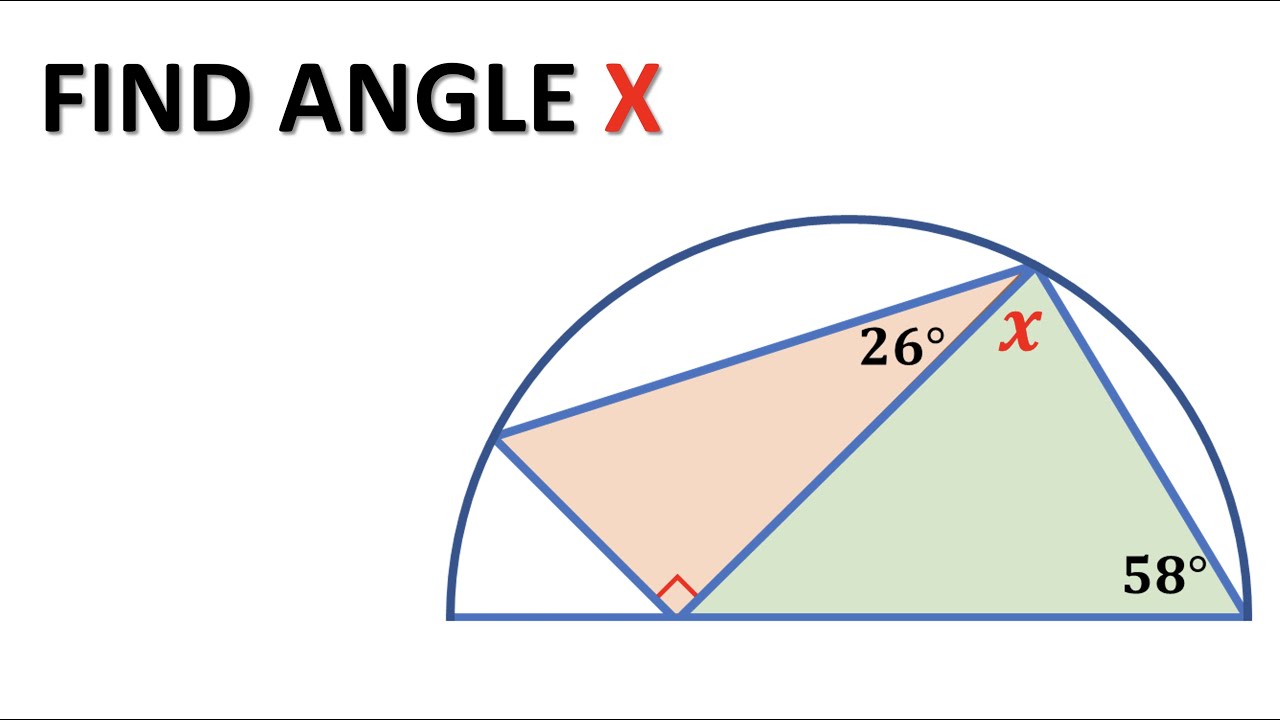
Показать описание
Additional information about inscribed angles and inscribed/cyclic quadrilaterals could be found here:
Find angle in a semicircle.
Angle Inscribed in a Semicircle
Circle Theorems - Angle in a semi circle IGCSE Revision
Angle Inscribed in a Semicircle
Can you find the value of angle X? | (Semicircle) | #math #maths | #geometry
Circle Theorem - Angle in a Semi Circle
Key Skill - Know that the angle in a semicircle is 90 degrees.
Everything About Circle Theorems - In 3 minutes!
2) Find angle 'alpha' in quadrant. #Class IX #Math #NCERT #CBSE Ch:9 Circles
How to Find The Missing Angle In the Semicircle | Geometry | Math
Angle in a Semicircle is 90 degrees | Circle Theorems #1
Angle in a Semi Circle
angle in a semicircle
Can you find Angle X in the Semicircle? | Fast & Easy Explanation
Angle in the semi circle (circle theorem) animation
Why angle in a semicircle is 90 degree?
Q3 Find angle in Triangle inscribed in a semicircle using Circle Theorem GCSE
10.6C--Inscribed Angle in a Semicircle
Find Angle X in this Semicircle | Step-by-Step Tutorial
Find The Missing Angle in the Semicircle | Geometry Puzzle |
Angle in a Semicircle contains right angle GCSE
The angle in a semicircle measures
Angle in a semicircle calculation
The angle in a semicircle is a right angle #shorts
Комментарии
 0:07:08
0:07:08
 0:02:02
0:02:02
 0:02:04
0:02:04
 0:03:33
0:03:33
 0:05:25
0:05:25
 0:01:19
0:01:19
 0:01:06
0:01:06
 0:04:11
0:04:11
 0:02:32
0:02:32
 0:02:56
0:02:56
 0:03:08
0:03:08
 0:05:00
0:05:00
 0:02:07
0:02:07
 0:03:46
0:03:46
 0:00:15
0:00:15
 0:00:15
0:00:15
 0:02:46
0:02:46
 0:06:34
0:06:34
 0:08:26
0:08:26
 0:08:14
0:08:14
 0:05:31
0:05:31
 0:00:55
0:00:55
 0:10:51
0:10:51
 0:00:38
0:00:38