filmov
tv
Find Angle X in this Semicircle | Step-by-Step Tutorial

Показать описание
Can you find the Angle X? | Quick & Simple Tutorial
Can You Find Angle X? | Geometry Challenge!
Challenge Question: Can you find the Angle X?| Step-by-Step Explanation
Calculate angle X in a 5-sided irregular Polygon | Learn how to Solve this Geometry problem Quickly
Find the angle X | How to Solve this Tricky Geometry problem Quickly
Can You Find Angle X? | Quick & Simple Explanation
Find the angle X in the Circle | Learn how to Solve this Tricky Geometry problem Quickly
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Single Phase Series AC Circuit Example
Find Angle X in the given Square | Quick & Simple Explanation
Finding the Missing Angle of a Triangle: A Step-by-Step Guide | Triangles | Math with Mr. J
Find Angle X for this Octagon! | Step-by-Step Explanation
Can you find Angle X in this given shape? | Step-by-Step Tutorial
Can you find the angle X in terms of Y? | (Triangle) | #math #maths | #geometry
Can you find the Value of Angle X? | Quick & Easy Explanation
Can you find the angle X? | (Polygon) | #math #maths | #geometry
Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon
Find the Value of x, and the Missing Angle Measures
Hard Problem | Find Angle x | PRMO RMO INMO IMO Math Olympiads SSC
Can you find angle X and Y values? | (Law of Sines) | #math #maths | #geometry
Missing Angles in Triangles | How to Find the Missing Angle of a Triangle Step by Step
Can you calculate the angle X? | (Justify your answer) | #math #maths | #geometry
Find Angle X in this Compound Figure Made of 2 Equilateral Triangles | Quick & Simple Explanatio...
Find the angle X | Japan Math Olympiad Geometry Problem
Комментарии
 0:04:44
0:04:44
 0:08:44
0:08:44
 0:08:05
0:08:05
 0:03:17
0:03:17
 0:06:42
0:06:42
 0:05:12
0:05:12
 0:03:39
0:03:39
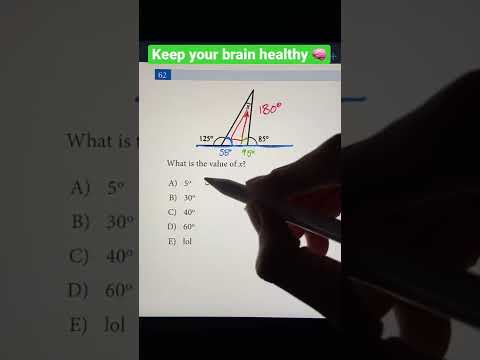 0:00:44
0:00:44
 0:06:43
0:06:43
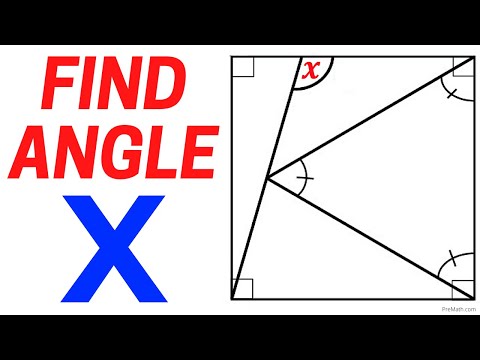 0:05:10
0:05:10
 0:05:14
0:05:14
 0:06:49
0:06:49
 0:04:01
0:04:01
 0:06:03
0:06:03
 0:06:05
0:06:05
 0:08:31
0:08:31
 0:07:00
0:07:00
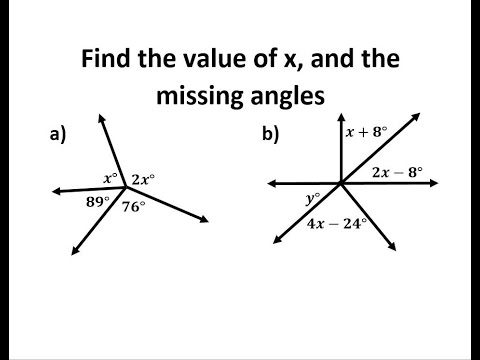 0:10:07
0:10:07
 0:05:13
0:05:13
 0:13:25
0:13:25
 0:03:40
0:03:40
 0:07:15
0:07:15
 0:06:24
0:06:24
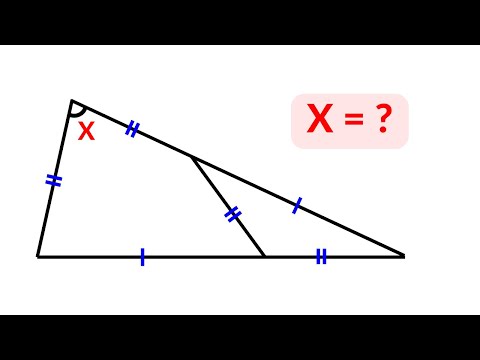 0:11:04
0:11:04