filmov
tv
Solving e³ˣ – e²ˣ = eˣ | The Golden Ratio
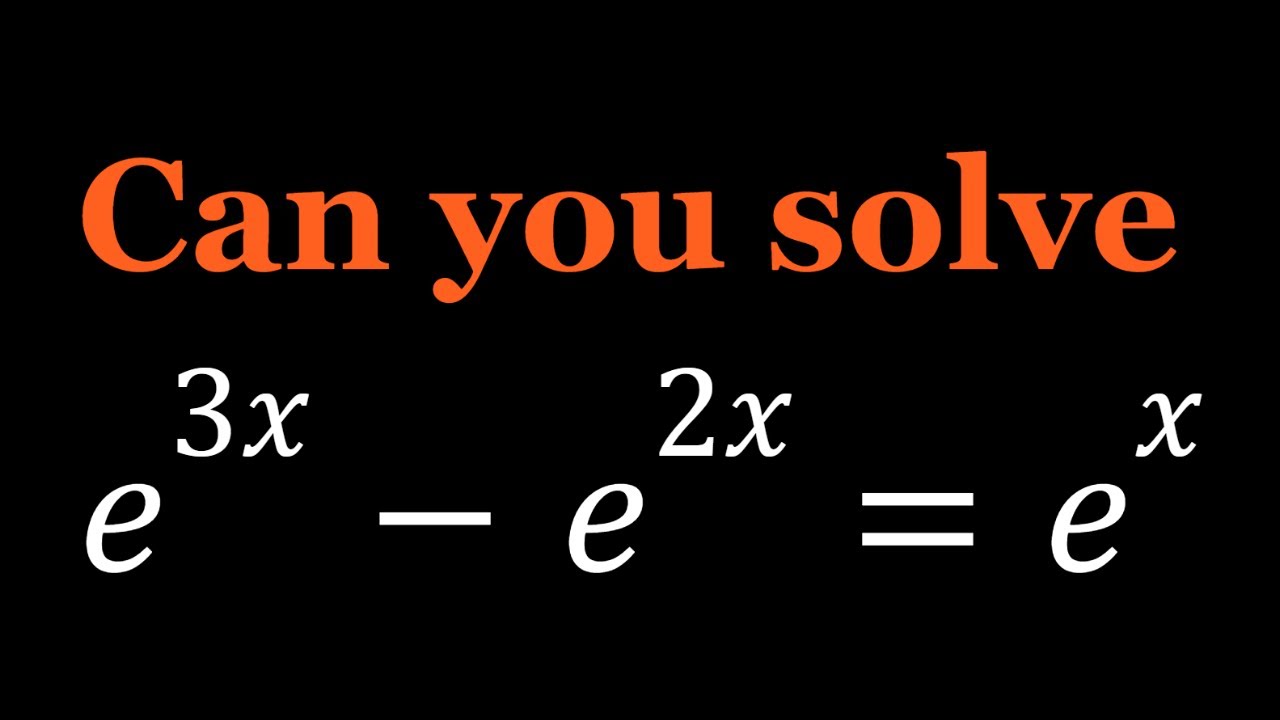
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving e³ˣ – e²ˣ = eˣ | The Golden Ratio
RÉSOUDRE e³ˣ = e²ˣ + eˣ
∫(e⁴ˣ + eˣ)/(e⁴ˣ + e³ˣ + e²ˣ + eˣ ) dx. Solve using substitution and algebra trick....
∫e³ˣ/(e⁴ˣ + e²ˣ + 1) dx [-∞, ∞]. Solve integral by inverting variable but without partial fraction....
Solving A Homemade Exponential Equation
Math olympiad | Can you solve this golden ratio problem ? | VIJAY Maths
Résolution de l'équation e^x+x+3=0, méthode analytique
A Homemade Exponential Equation
Amazing Equation Give the Answer as Golden Ratio
Simplifying A Log Expression | A Formula
16. SOLVE ( D³ - 5D² + 7D - 3)y = e²ˣ coshx.
VIDÉO DE RENTRÉE 😁
A Functional Equation | Can you find g(x)?
Solving x^{4x^8}=2 | Math Competitions
Math Olympiad Challenge 8^x-2^x/4^x-2^x=17 | Nice Method
Une équation exponentielle intéressante : e^x=x^e
Simplifying A Rational Expression | Polynomials
RÉSOUDRE 6! × 7! = x!
2³ˣ + 2ˣ = 222, le niveau monte MAIS TU SAIS TOUT FAIRE
RÉSOUDRE 1/x + 1/y = 1/10
Integrate x ^ 2 * (1 - 2/x) ^ 2 dx
Je découvre une propriété RÉVOLUTIONNAIRE... pour moi 😅
A Rational Equation | Math Olympiads
Golden Ratio in Continued Fraction #goldennumber #goldenratio #mathematics
Комментарии
 0:09:29
0:09:29
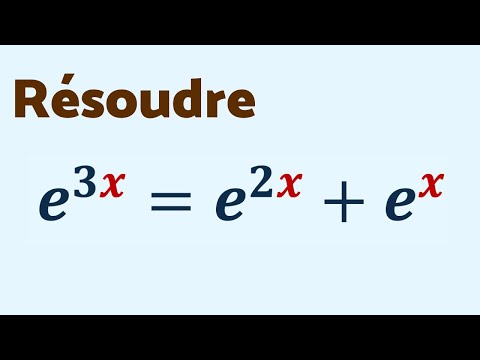 0:08:10
0:08:10
 0:02:30
0:02:30
 0:04:13
0:04:13
 0:09:01
0:09:01
 0:14:30
0:14:30
 0:09:09
0:09:09
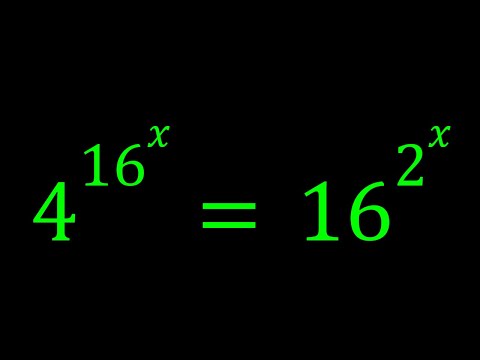 0:04:51
0:04:51
 0:03:25
0:03:25
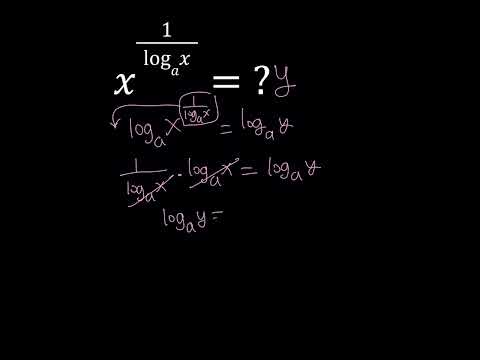 0:00:35
0:00:35
 0:13:16
0:13:16
 0:06:12
0:06:12
 0:04:22
0:04:22
 0:08:50
0:08:50
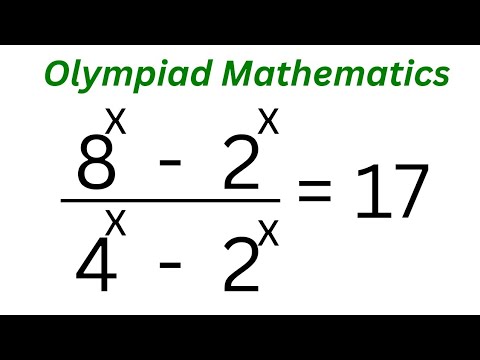 0:06:04
0:06:04
 0:03:33
0:03:33
 0:09:19
0:09:19
 0:04:36
0:04:36
 0:08:53
0:08:53
 0:10:10
0:10:10
 0:02:35
0:02:35
 0:07:54
0:07:54
 0:10:47
0:10:47
 0:00:33
0:00:33