filmov
tv
Can you solve This If-Then Algebraic Question? | Step-by-Step Explanation

Показать описание
Learn how to solve this If-Then question:
If a + b = 2 and 1/a + 1/b =2
Then a^3 + b^3 = ?
If a + b = 2 and 1/a + 1/b =2
Then a^3 + b^3 = ?
Can you solve This If-Then Algebraic Question? | Step-by-Step Explanation
Can You Solve this If-Then Math Problem? | Step-by-Step Tutorial
Can You Solve this If-Then Math Problem? | Math Challenge!
Can you solve this If-Then Exponential Problem? | Fast & Easy Explanation
Can you solve this If Then Math Puzzle?
Can you solve this IF THEN MATH PUZZLE?
Can You Solve this If-Then Multivariable System of Equations Problem? | Step-by-Step Tutorial
Can You Solve this If-Then Problem? | Radicals & Negative Exponents!
Can You Solve these If-Then Radical Equations? | Step-by-Step Explanation
Can you solve for the mystery number?
If you can solve all of them then you’re a genius
If Then Math Puzzle I Can you solve this?
Solve this Polynomial If-Then Statement | Simple & In-Depth Explanation
Solve this IF-THEN Problem in 1 Minute | NO Calculators!
If you can solve this, you can be an engineer.
Solve this Exponential If-Then Problem | Step-by-Step Tutorial
If You Can Solve This Riddle, You’re Smarter Than Average #shorts
If you are a genius solve this! Math Game Challenge!!!
A $100,000 Math Problem Only 1% Can Solve
You are a math genius if you can solve this marble question
Can you solve this? If You are not getting the answer then check the discription box👍👍
If You Can Solve This Riddle, You're A Psychopath
Can you Solve this Challenging Algebraic If-Then problem | Math Olympiad
ll can you solve it if question solve ll #mathematics #maths #mathpuzzle #iqtest
Комментарии
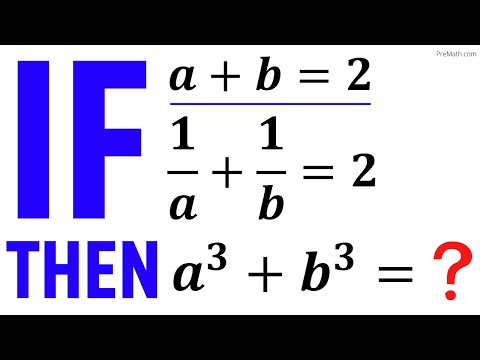 0:04:34
0:04:34
 0:04:38
0:04:38
 0:06:11
0:06:11
 0:06:06
0:06:06
 0:01:01
0:01:01
 0:01:01
0:01:01
 0:10:55
0:10:55
 0:08:05
0:08:05
 0:10:14
0:10:14
 0:08:56
0:08:56
 0:02:59
0:02:59
 0:01:01
0:01:01
 0:09:25
0:09:25
 0:02:45
0:02:45
 0:08:40
0:08:40
 0:08:53
0:08:53
 0:00:35
0:00:35
 0:00:28
0:00:28
 0:11:14
0:11:14
 0:04:09
0:04:09
 0:00:12
0:00:12
 0:01:00
0:01:00
 0:04:29
0:04:29
 0:00:06
0:00:06