filmov
tv
Three pretty geometric theorems, proved by complex numbers

Показать описание
Bottema'a theorem, van Aubel's theorem and Napoleon's theorem, are all brilliant. If you have never seen them before, you will be amazed! I prove then all by working in the complex plan, as van Aubel did in 1878.
Monge's Theorem
A Beautiful Proof of Ptolemy's Theorem.
Everything About Circle Theorems - In 3 minutes!
Triangle Congruence Theorems, Two Column Proofs, SSS, SAS, ASA, AAS Postulates, Geometry Problems
Stewarts theorem: Three Collinear points, Proof & derivation, Geometry Straight lines & tria...
ANGLE THEOREMS - Top 10 Must Know
8 theorems on circle in 2 min | mathocube |
Triangle Congruence Theorems Explained: ASA, AAS, HL
How Euclid Proved the Pythagorean Theorem
Only U.S. President to prove a theorem
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Geometry, Two Column Proofs of Angles - Addition, Substitution & Transitive Property
Viviani’s Theorem II
Proof: Sum of measures of angles in a triangle are 180 | Geometry | Khan Academy
Angle at Centre Theorem: Proof
Circle Theorems - GCSE Higher Maths
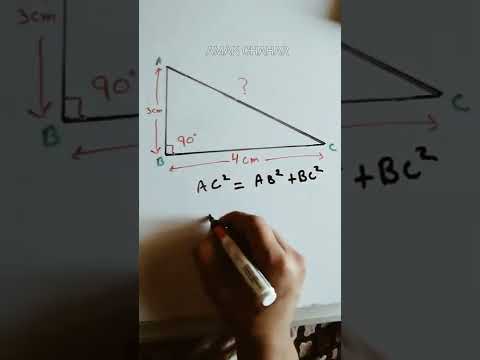
Pythagoras theorem
Pythagorean Theorem: Six Proofs
Proving Circle Theorems: 5 Proofs in 10 minutes
Proof: Triangle Midsegment Theorem | Geometry, Proofs
Thales Theorem ll Basic Proportionality Theorem ll Class 10 Maths
Every Circle Theorem with Animations. #geometry
A Visual Proof of the Pythagorean Theorem
How to find Right angle triangle Side :- Pythagoras theorem
Комментарии
 0:00:59
0:00:59
 0:04:12
0:04:12
 0:04:11
0:04:11
 0:50:27
0:50:27
 0:05:50
0:05:50
 0:20:47
0:20:47
 0:01:44
0:01:44
 0:07:25
0:07:25
 0:00:48
0:00:48
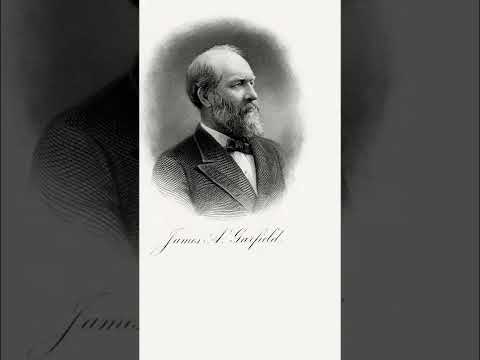 0:01:00
0:01:00
 0:17:08
0:17:08
 0:11:41
0:11:41
 0:01:00
0:01:00
 0:04:28
0:04:28
 0:04:05
0:04:05
 0:13:53
0:13:53
 0:00:16
0:00:16
 0:01:00
0:01:00
 0:14:27
0:14:27
 0:08:16
0:08:16
 0:00:10
0:00:10
 0:01:00
0:01:00
 0:00:40
0:00:40
 0:00:27
0:00:27