filmov
tv
Visualising Pythagoras: ultimate proofs and crazy contortions
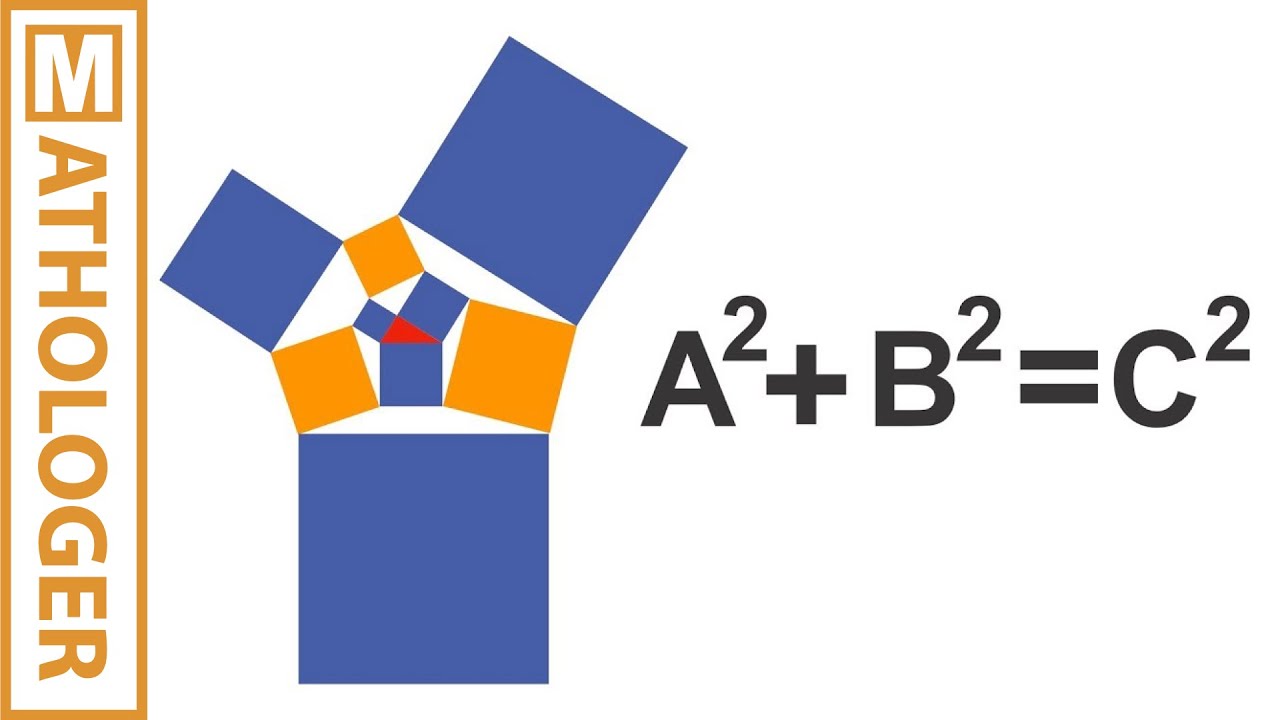
Показать описание
NEW (Christmas 2019). Two ways to support Mathologer
(see the Patreon page for details)
Finally, a Mathologer video about Pythagoras. Featuring some of the most beautiful and simplest proofs of THE theorem of theorems plus an intro to lots of the most visually stunning Pythagoranish facts and theorems from off the beaten track: the Pythagoras Pythagoras (two words :), 60 and 120 degree Pythagoras, de Gua's theorem, etc.
Things to check out:
As usual thank you very much to Marty and Danil for all their help with this video.
Enjoy!
(see the Patreon page for details)
Finally, a Mathologer video about Pythagoras. Featuring some of the most beautiful and simplest proofs of THE theorem of theorems plus an intro to lots of the most visually stunning Pythagoranish facts and theorems from off the beaten track: the Pythagoras Pythagoras (two words :), 60 and 120 degree Pythagoras, de Gua's theorem, etc.
Things to check out:
As usual thank you very much to Marty and Danil for all their help with this video.
Enjoy!
Visualising Pythagoras: ultimate proofs and crazy contortions
Pythagoras’ theorem, an animated explanation!
Pythagorean Theorem: Six Proofs
Pythagorean Theorem II (visual proof)
How many ways are there to prove the Pythagorean theorem? - Betty Fei
Visual Proof of Pythagoras' Theorem
Pythagoras Would Be Proud: High School Students' New Proof of the Pythagorean Theorem [TRIGONOM...
Demonstrating Pythagoras' theorem using a clever gadget - QI: Series M Episode 5 Preview - BBC ...
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Ten Epic Pythagorean Proofs Without Words
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Visualizing Pythagoras Theorem | Learn with BYJU'S
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
When mathematicians get bored (ep1)
Visual Proof of the Pythagorean Theorem - Visualizing Algebra
'So close 🤏🏼,yet so far ♾️' Explanation and code in description #maths #satisfying #adhd #...
The Pythagorean Theorem FAVORITE PROOF
Pythagoras Theorem Visual Proof under 3 mins
Proof of the Pythagorean Theorem in 3 Dimensions
18 year old students just discovered a proof of Pythagoras that mathematicians said was impossible
Pythagoras' theorem and proof (cut-out demo)
Proving God exists using Math
All 6 Trig Functions on the Unit Circle
Pythagoras twisted squares: Why did they not teach you any of this in school?
Комментарии
 0:21:01
0:21:01
 0:00:40
0:00:40
 0:01:00
0:01:00
 0:01:26
0:01:26
 0:05:17
0:05:17
 0:11:14
0:11:14
 0:13:57
0:13:57
 0:01:30
0:01:30
 0:00:38
0:00:38
 0:08:01
0:08:01
 0:00:19
0:00:19
 0:00:42
0:00:42
 0:04:15
0:04:15
 0:00:37
0:00:37
 0:02:19
0:02:19
 0:01:00
0:01:00
 0:01:41
0:01:41
 0:02:36
0:02:36
 0:05:02
0:05:02
 0:18:07
0:18:07
 0:01:30
0:01:30
 0:05:23
0:05:23
 0:08:19
0:08:19
 0:38:33
0:38:33