filmov
tv
Sum of Prime Squares is a Cube

Показать описание
Sum of Prime Squares is a Cube
When is a prime the sum of two squares? — The Ross Program
The Reciprocal Prime Series (this proof should be taught in calculus!)
when is the sum of squares a power of a prime??
The Prime Problem with a One Sentence Proof - Numberphile
The Prime Number Race (with 3Blue1Brown) - Numberphile
HP Prime - Correlation and Regression - Sum of the Squared Residuals
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
Real Numbers FULL CHAPTER | Math NCERT Solution Class 10 Chapter 1 Concept PYQs, Important Questions
Prime Numbers - Magic Trick!! - Part 1 | Fun Math | Don't Memorise
Return two prime numbers gfg problem of the day | 2 prime numbers whose sum equals given number
The sum of all the prime numbers from 1 to 20 is? #shorts
The Most Wanted Prime Number - Numberphile
Pi hiding in prime regularities
Find total number of prime factors | Important trick for GMAT, CAT, SAT, BankPO, etc #primefactors
Pillai: Ramanujan's Formula on the Sum of Squares of Prime Inverses (~ 0.455945326) Ramanujan
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Prime Reciprocal Series with @blackpenredpen (Oxford Maths Interview Question)
What are Prime Numbers? | Math with Mr. J
#How to find prime numbers between 1-100 in 5 seconds#For competitive exams#short#shorts
The sum of the prime numbers between 60 and 75\nis\n(a) 199 \n(b) 201 (c) \n211 (d) 272 | 6 | PL...
C Program To Express A Number as Sum of Two Prime Numbers
PotW: Sum of Prime Factors [Factorization]
Prime Numbers Made of Just the Digit 1... #shorts
Комментарии
 0:08:15
0:08:15
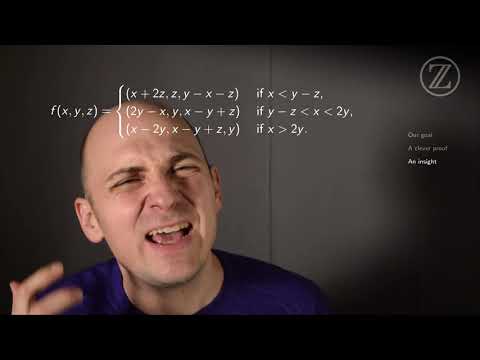 0:09:57
0:09:57
 0:11:44
0:11:44
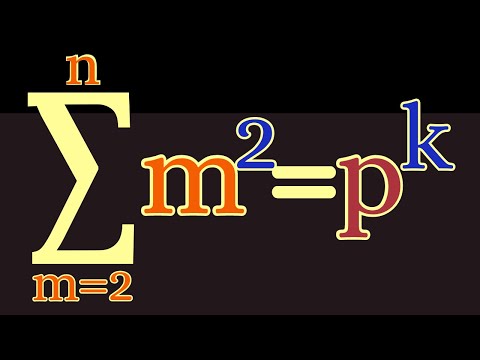 0:16:44
0:16:44
 0:06:42
0:06:42
 0:20:29
0:20:29
 0:04:40
0:04:40
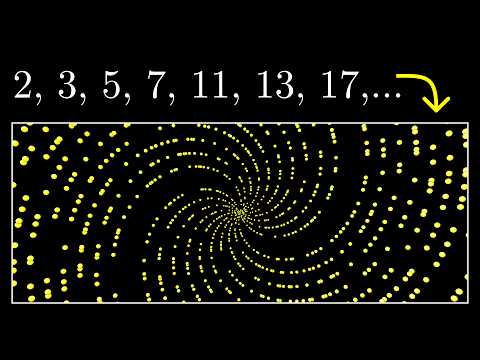 0:22:21
0:22:21
 0:55:50
0:55:50
 0:00:39
0:00:39
 0:16:27
0:16:27
 0:00:07
0:00:07
 0:08:35
0:08:35
 0:30:42
0:30:42
 0:08:02
0:08:02
 0:19:44
0:19:44
 0:17:08
0:17:08
 0:22:09
0:22:09
 0:04:46
0:04:46
 0:00:38
0:00:38
 0:01:32
0:01:32
 0:14:02
0:14:02
 0:04:28
0:04:28
 0:00:55
0:00:55