The Dimension of a Subspace | Definition + First Examples

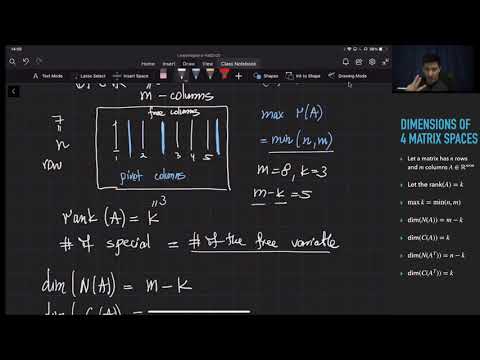
What, exactly, is dimension? We all say that R^3, the space we live in, is three dimensional. But what about the dimension of a generic subspace? In this video we use the number of basis vectors to define the dimension of a subspace, and work through several examples.

**************************************************
Now it's your turn:
1) Summarize the big idea of this video in your own words
2) Write down anything you are unsure about to think about later
3) What questions for the future do you have? Where are we going with this content?
4) Can you come up with your own sample test problem on this material? Solve it!

Learning mathematics is best done by actually DOING mathematics. A video like this can only ever be a starting point. I might show you the basic ideas, definitions, formulas, and examples, but to truly master math means that you have to spend time - a lot of time! - sitting down and trying problems yourself, asking questions, and thinking about mathematics. So before you go on to the next video, pause and go THINK.

***************************************************
Want more ideas for learning math effectively?
►How to Watch Math Videos:

****************************************************
►Want some cool math? Check out my "Cool Math" Series:

****************************************************
Course Playlists:

*****************************************************
*****************************************************

This video was created by Dr. Trefor Bazett, an Assistant Professor, Educator at the University of Cincinnati.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[kevinmak]

don't know if you'll ever read this but i am really thankful for these videos

[fatimashehryar]

Thanks Plz also upload a lecture up on linear transformation using therom10 in exercise 3.3

[brendonchen]

I had a problem ask: S is a subspace of a 4x4 matrix consisting of lower triangular matrices, What is the dim(S). The answer is 10; however this is a higher dimension compared to the 4x4 matrix, how is this possible?

[mirzaaghaalikhan]

Sir I have a problem, I am AI student, and I went through you LinAlgebra series, you used the columns as a count of dimension of space, I mean if there is a 3D matrix then it has 3 columns of basis vectors. But now when I started to learn NumPy, it uses rows as its dimension count. I am confused.
Also I searched on stack exchange but it says that *dimension is defined as the **_the minimum number of coordinates required to express a point in space_*

What is wrong here, plz help me out. I am very keen to learn basics as they are always so confusing. Thanks

[tasninnewaz]

Sir, Animation or Visualization is better than hand writting