filmov
tv
Extreme Value Theorem (Proof) | Maximum and Minimum Values Theorem | Continuity | Advanced Calculus

Показать описание
#MathsClass #LearningClass #ExtremeValueTheorem #Proof #MaximumandMinimumValuesTheorem #Mathematics #AdvancedCalculus #Maths #Calculus #ContinuityofaFunction
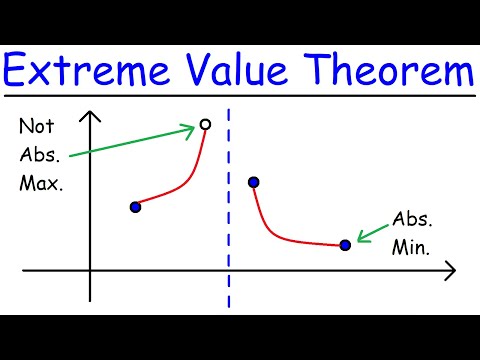
EXTREME VALUE THEOREM: In calculus, the extreme value theorem states that if a real-valued function f is continuous on the closed interval [a, b], then f must attain a maximum and a minimum, each at least once. It is sometimes also known as Maximum and Minimum Values Theorem.
APPLICATION OF THE THEOREM: The extreme value theorem enriches the boundedness theorem by saying that not only is the function bounded, but it also attains its least upper bound as its maximum and its greatest lower bound as its minimum.
The extreme value theorem is used to prove Rolle's theorem. In a formulation due to Karl Weierstrass, this theorem states that a continuous function from a non-empty compact space to a subset of the real numbers attains a maximum and a minimum.
EXTREME VALUE THEOREM: In calculus, the extreme value theorem states that if a real-valued function f is continuous on the closed interval [a, b], then f must attain a maximum and a minimum, each at least once. It is sometimes also known as Maximum and Minimum Values Theorem.
APPLICATION OF THE THEOREM: The extreme value theorem enriches the boundedness theorem by saying that not only is the function bounded, but it also attains its least upper bound as its maximum and its greatest lower bound as its minimum.
The extreme value theorem is used to prove Rolle's theorem. In a formulation due to Karl Weierstrass, this theorem states that a continuous function from a non-empty compact space to a subset of the real numbers attains a maximum and a minimum.
Can you prove it? The Extreme Value Theorem
Extreme Value Theorem Proof
Proof of the Extreme Value Thm
Extreme Value Theorem
Extreme Value Theorem (Proof) | Maximum and Minimum Values Theorem | Continuity | Advanced Calculus
The Extreme Value Theorem | Calculus
Extreme value theorem | Existence theorems | AP Calculus AB | Khan Academy
The Extreme Value Theorem - Proof
The Extreme Value Theorem
M 08 05 ** Proof of the Extreme Value Theorem **
402.4Y2 Compact Sets and the Extreme Value Theorem
Proving Rolle's Theorem using the Extreme Value Theorem
Extreme Value Theorem --- Part 1
Real Analysis Lecture 18 Part 1: The extreme value theorem
The Extreme Value Theorem - Real Analysis | Lecture 13
Real Analysis | Where are extreme values?
Intuitive Topology 13: Intermediate & Extreme Value Theorems
Extreme Value Theorem Introduction
Extreme Value Theorem Part 1
Extreme Value Theorem
Extreme Value Theorem
5.3 Proof of the Local Extreme Value Theorem
Intro Real Analysis 13: Prove Extreme Value Theorem, Intermediate Value Property, Uniform Continuity
Calculus I: Extreme Value Theorem
Комментарии
 0:18:11
0:18:11
 0:06:45
0:06:45
 0:06:13
0:06:13
 0:06:04
0:06:04
 0:11:29
0:11:29
 0:09:13
0:09:13
 0:07:58
0:07:58
 0:22:09
0:22:09
 0:32:25
0:32:25
 0:18:16
0:18:16
 0:15:14
0:15:14
 0:12:56
0:12:56
 0:04:28
0:04:28
 0:06:02
0:06:02
 0:35:05
0:35:05
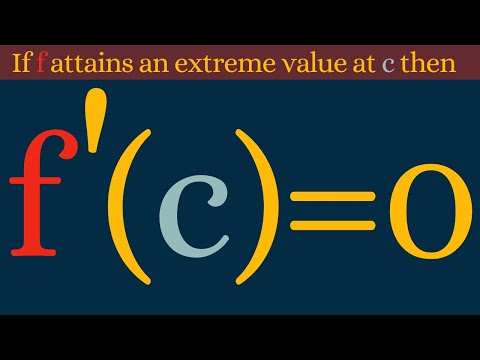 0:08:25
0:08:25
 0:14:29
0:14:29
 0:02:49
0:02:49
 0:23:19
0:23:19
 0:09:18
0:09:18
 0:06:01
0:06:01
 0:03:23
0:03:23
 0:36:37
0:36:37
 0:15:46
0:15:46