The Extreme Value Theorem | Calculus

preview_player
Показать описание
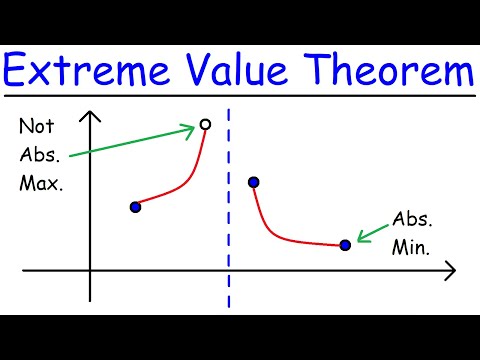
We introduce the Extreme Value Theorem, which states that if f is a continuous function on a closed interval [a,b], then f takes on a maximum f(c) and a minimum f(d) at points c and d in the interval [a,b]. We also discuss critical points/critical numbers and their importance to finding extreme values. We then look at several examples of continuous and discontinuous functions where the EVT does and doesn't apply. We finish with a basic set of Extreme Value Theorem problems.

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Extreme Value Theorem 0:06:04

Extreme Value Theorem

Extreme value theorem 0:07:58

Extreme value theorem | Existence theorems | AP Calculus AB | Khan Academy

The Extreme Value 0:09:13

The Extreme Value Theorem | Calculus

The Extreme Value 0:06:15

The Extreme Value Theorem and How to Use it in Calculus

Calculus AB/BC – 0:14:50

Calculus AB/BC – 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points

Extreme Value Theorem, 0:00:44

Extreme Value Theorem, Definition - AP Calculus BC

Finding Absolute Maximum 0:17:17

Finding Absolute Maximum and Minimum Values - Absolute Extrema

Extreme Value Theorem: 0:05:40

Extreme Value Theorem: Finding Absolute Extrema on a Closed Interval ❖ Calculus

No likelihood? No 0:54:19

No likelihood? No problem! — Bayesian Statistics in R

03.1 - Extreme 0:18:08

03.1 - Extreme Value Theorem

Can you prove 0:18:11

Can you prove it? The Extreme Value Theorem

Example of Extreme 0:02:52

Example of Extreme Value Theorem 1

Extreme Value Theorem 0:04:28

Extreme Value Theorem --- Part 1

The Extreme Value 0:35:05

The Extreme Value Theorem - Real Analysis | Lecture 13

THE INTERMEDIATE VALUE 0:31:10

THE INTERMEDIATE VALUE AND THE EXTREME VALUE THEOREMS || BASIC CALCULUS

Extreme Value Theorem 0:01:08

Extreme Value Theorem - Calculus

The Extreme Value 0:09:14

The Extreme Value Theorem

The Extreme Value 0:05:30

The Extreme Value Theorem, an application of derivatives

EXTREME VALUE THEOREM 0:17:34

EXTREME VALUE THEOREM Sir Ric

Define absolute extrema 0:01:25

Define absolute extrema and understand the extreme value theorem

Extreme Value Theorem 0:05:42

Extreme Value Theorem / Calculus / Interactive Video

The Extreme Value 0:07:22

The Extreme Value Theorem and an Outline of How to Apply It

Real Analysis Ep 0:48:48

Real Analysis Ep 27: Extreme value theorem

EXTREME VALUE THEOREM 0:10:49

EXTREME VALUE THEOREM - Examples showing how to use the extreme value theorem | Jake's Math Les...

Комментарии
Автор

Love your tutorials man could you please give excersises after the tutorials to try and solve

edithanyaibe
Автор

A proof of this in the real analysis series would be nice, i looked online but it seems it uses Bolzano-Weirstrass and it gets a bit confusing. Thnx for your great content

wannabehuman.production
Автор

Thank you very much. I have a Calculus exam soon

ayah_qreshat
welcome to shbcf.ru