Calc 1, Lec 15B: Visualizing Local Linearity (or Lack Thereof), Infinitesimal Calculus Introduction

(0:00) Lecture 15B includes one of my favorite topics.
(0:18) Review differentiability. A proof that if a function is differentiable at a point, then it is continuous at that point.
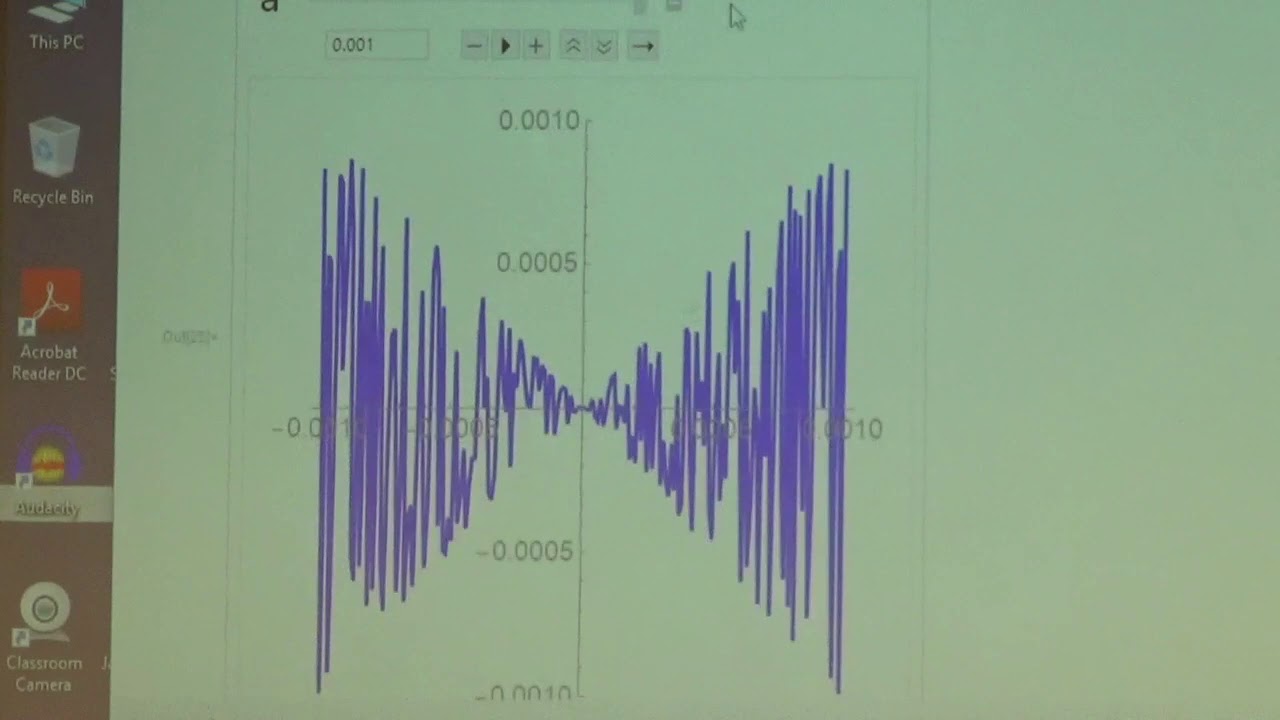
(6:16) Local linearity and Mathematica visuals (zoom in to the graphs).
(11:16) Calculus sans (without) limits (Infinitesimal Calculus). This is an intuitive approach, not a rigorous approach. It is a good approach to use for scientists and engineers. It can be made rigorous in the subject of nonstandard analysis.
(14:03) Example 1: find dy in terms of dx when y = f(x) = x^2. Ignore dx^2. Use this to find the derivative dy/dx.
(21:45) Example 2: find dy in terms of dx when y = x^3. Ignore terms involving dx^2 and dx^3. Use this to find the derivative dy/dx.
(23:54) Example 3: find dy in terms of dx when y = sin(x). Need a trigonometric identity. Also replace cos(dx) by 1 and sin(dx) by dx (reasons for this to be given in Lecture 16A).