filmov
tv
Tutorial: Periodic trajectories in billiards - and where to find them

Показать описание
This talk is about finding periodic trajectories in convex billiards. It states in particular a version of the Poincaré-Birkhoff theorem for twist maps, which can be applied to show existence of such trajectories. Two ways of proving this theorem are sketched.
Periodic trajectories: 0:00
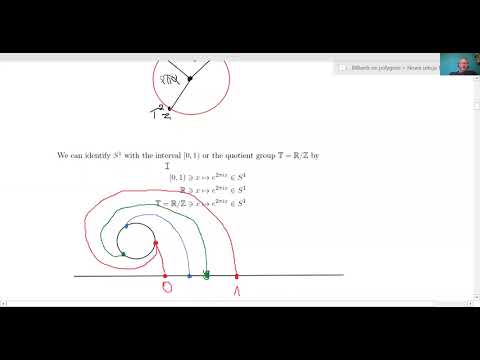
Billiard in a circle: 5:05
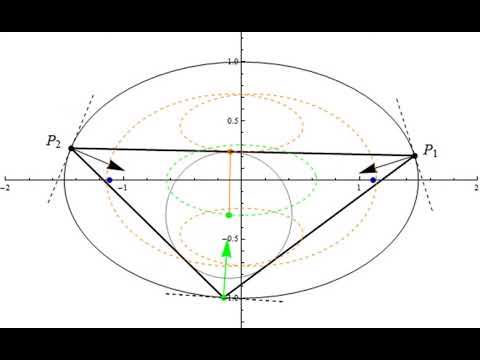
From circle to ellipse: 15:34
General convex billiard: 18:58
The Poincaré-Birkhoff theorem: 23:30
Poincaré and Birkhoff: 25:18
Continuity: 27:00
First proof: 32:18
Generating function: 42:31
Second proof: 54:52
Area preservation: 1:06:49
The original formulations of the Poincaré-Birkhoff theorem is the following (see for instance Appendix 9 in the book by V.I. Arnold): Suppose we are given an area-preserving map of the planar annulus into itself, which is homeomorphic (meaning continuous, invertible, with continous inverse). Assume that the boundary circles are turned into different directions by the map. Then this map has at least two fixed points.
One finds several different versions and proofs of this result in the literature. An overview on the results on orbits with given rotation number can be found in the article by J.D. Meiss, see references below.
The first proof I give in the talk is not quite complete. For rotation number 1/2, it shows that T^2 has at least two fixed points. But these fixed points could belong to the same orbit of period 2. The second proof I give does show the existence of a second orbit. A possible way to complete the first proof is to consider the behavior of the orbits near the two fixed points, which is different. In one case, the orbits tend to rotate around the fixed point, which is typically elliptic. In the other case, they are attracted in one direction, and repelled in the other one, making the point hyperbolic. It follows that the two fixed points cannot be the image of one another. Hence the two curves in the first proof have to intersect at least 4 times - but perhaps a stronger assumption such as differentiability of the map is needed.
References:
V. I. Arnold , Mathematical Methods of Classical Mechanics
Springer, Graduate Texts in Mathematics (GTM, volume 60, 1978)
J. D. Meiss, Symplectic maps, variational principles, and transport
Rev. Mod. Phys. 64, 795 (1992)
#billiard #billiards #chaos #periodic #periodicity
Periodic trajectories: 0:00
Billiard in a circle: 5:05
From circle to ellipse: 15:34
General convex billiard: 18:58
The Poincaré-Birkhoff theorem: 23:30
Poincaré and Birkhoff: 25:18
Continuity: 27:00
First proof: 32:18
Generating function: 42:31
Second proof: 54:52
Area preservation: 1:06:49
The original formulations of the Poincaré-Birkhoff theorem is the following (see for instance Appendix 9 in the book by V.I. Arnold): Suppose we are given an area-preserving map of the planar annulus into itself, which is homeomorphic (meaning continuous, invertible, with continous inverse). Assume that the boundary circles are turned into different directions by the map. Then this map has at least two fixed points.
One finds several different versions and proofs of this result in the literature. An overview on the results on orbits with given rotation number can be found in the article by J.D. Meiss, see references below.
The first proof I give in the talk is not quite complete. For rotation number 1/2, it shows that T^2 has at least two fixed points. But these fixed points could belong to the same orbit of period 2. The second proof I give does show the existence of a second orbit. A possible way to complete the first proof is to consider the behavior of the orbits near the two fixed points, which is different. In one case, the orbits tend to rotate around the fixed point, which is typically elliptic. In the other case, they are attracted in one direction, and repelled in the other one, making the point hyperbolic. It follows that the two fixed points cannot be the image of one another. Hence the two curves in the first proof have to intersect at least 4 times - but perhaps a stronger assumption such as differentiability of the map is needed.
References:
V. I. Arnold , Mathematical Methods of Classical Mechanics
Springer, Graduate Texts in Mathematics (GTM, volume 60, 1978)
J. D. Meiss, Symplectic maps, variational principles, and transport
Rev. Mod. Phys. 64, 795 (1992)
#billiard #billiards #chaos #periodic #periodicity
Комментарии
 1:12:35
1:12:35
 0:02:01
0:02:01
 0:20:12
0:20:12
 0:08:36
0:08:36
 0:03:40
0:03:40
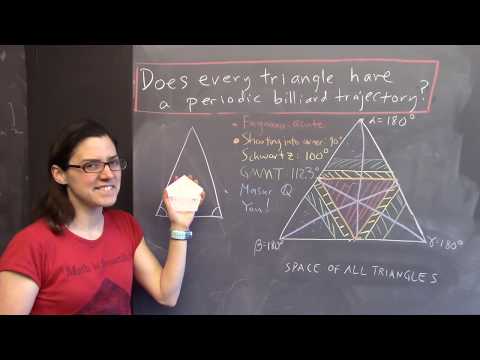 0:04:49
0:04:49
 0:02:09
0:02:09
 0:11:58
0:11:58
 0:00:45
0:00:45
 0:09:44
0:09:44
 0:04:01
0:04:01
 0:59:46
0:59:46
 1:00:46
1:00:46
 0:11:58
0:11:58
 0:04:01
0:04:01
 0:02:15
0:02:15
 0:06:46
0:06:46
 0:10:40
0:10:40
 0:01:25
0:01:25
 1:06:56
1:06:56
 0:00:24
0:00:24
 0:01:17
0:01:17
 1:41:17
1:41:17
 0:00:25
0:00:25