Proof: Medians Cut a Triangle into Six Equal Area Triangles | Geometry, Medians, Proofs

How do we prove that the three medians of a triangle cut the triangle into six triangles with equal areas? We go over this verbose statement in today's geometry proof video!

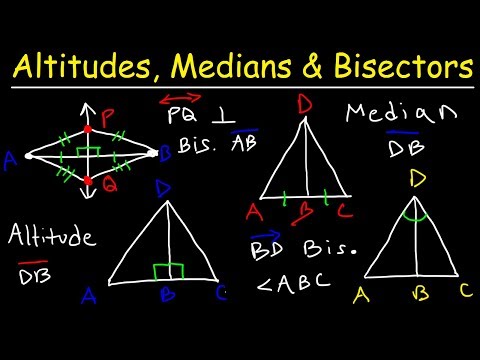
Remember that a median of a triangle is a line segment with one endpoint at a vertex of the triangle, and the other endpoint on the midpoint of the opposite side. The three medians of a triangle always intersect at one point inside the triangle (thus creating the six triangles we will be analyzing), which we assume and do not prove in this video.

The proof proceeds using an equal base, equal height, therefore equal area argument, over and over until we have proven all of the areas are equal! There is a little bit of algebra involved, but the main challenge is identifying the equal bases and heights of triangles that will help us prove our desired result! Watch the video lesson for the detailed walkthrough!

I hope you find this video helpful, and be sure to ask any questions down in the comments!

+WRATH OF MATH+

Follow Wrath of Math on...