Proof : Centroid Divides Median in 2:1 Ratio | Trigonometry | Basic Concept | IIT | Edusaral

preview_player
Показать описание
Topic - Proof : Centroid Divides Median in 2:1 Ratio | Trigonometry | Basic Concept | IIT | MPREPIIT34 | Edusaral

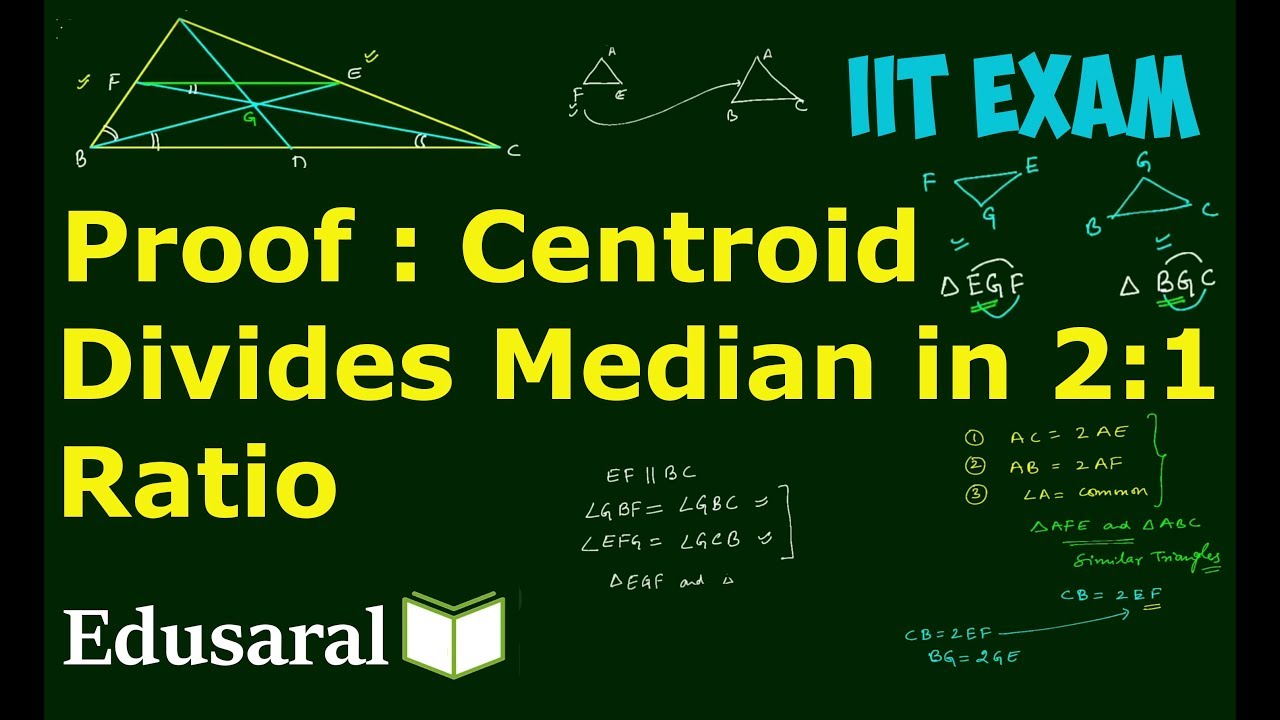
Learn : Prove that how Centroid Divides Median in 2:1 Ratio ?

JOIN US ON :-

PLAYLISTs



Test Preparation

Team Edusaral
  1. Edusaral
  2. MPREPIIT34
  3. IIT
  4. Centroid Divides Median in 2:1 Ratio
  5. Trigonometry
  6. Trigonometry- Centroid Divides Median in 2:1 Ratio
Рекомендации по теме
Centroid of a 0:02:49

Centroid of a triangle divides a median in the ratio 2:1.

Proof: centroid divide 0:07:12

Proof: centroid divide the median in the ratio 2:1 from the vertex

Proving that the 0:06:56

Proving that the centroid is 2-3rds along the median | Geometry | Khan Academy

Prove that Centroid 0:09:13

Prove that Centroid divides Medians in the ratio of 2:1

Proof : Centroid 0:06:05

Proof : Centroid Divides Median in 2:1 Ratio | Trigonometry | Basic Concept | IIT | Edusaral

Why Does Centroid 0:09:56

Why Does Centroid of a Triangle Divides Median into 2:1?

Proof - How 0:08:25

Proof - How centroid divides median in 2:1 ?

CENTROID divides the 0:10:01

CENTROID divides the medians in 2:1 ratio || PROOF ||

Visual Proof of 0:00:59

Visual Proof of centroid dividing median in ratio 2:3

VISUAL PROOF | 0:10:30

VISUAL PROOF | Centroid Divides the Median in Ratio of 2:1 | Using ANIMATION Tools | CREATA CLASSES

centroid divides median 0:15:57

centroid divides median in the ratio of 2:1, How to prove? watch description also 👇👇👇

Medians divide into 0:07:46

Medians divide into smaller triangles of equal area | Geometry | Khan Academy

Vectors Centroid Divides 0:10:35

Vectors Centroid Divides Median in the Ratio 2 to 1 Prove Zero Vector Sum MCV4U Edexcel Math 2

MATHEMATICAL PROOFS || 0:08:24

MATHEMATICAL PROOFS || PROOF OF CENTROID DIVIDES MEDIAN IN THE RATIO 2 : 1 || BY VINAY

Centroid divides the 0:07:52

Centroid divides the median in the ratio of 1: 2

centroid divides medians 0:01:00

centroid divides medians 2:1 coordinate of centroid

Find Centroid Intersection 0:18:25

Find Centroid Intersection of Medians and Show that it divides median in ratio 2 to 3

How to prove 0:04:54

How to prove centroid divides medians 2:1..by so easy method..ohm sai

Centroid of a 0:00:59

Centroid of a Triangle #jeedailyconcepts #trigonometry

The Centroid of 0:09:02

The Centroid of a Triangle Using Vectors

Centroid (One Third 0:02:40

Centroid (One Third Two Thirds) Examples

Magical Geometry | 0:00:15

Magical Geometry | Centroid of a Triangle

Concurrence of Medians 0:08:09

Concurrence of Medians (1 of 2: Proof via similar triangles)

Ratio in which 0:00:58

Ratio in which centroid divides the median

Комментарии
Автор

Simpler would be to drop medians from B and C intersecting at G join A and G produce it outside triangle, draw a line parallel to CG through B interesting AG at D, join DC. Since CG is parallel to BD, take triangle ABD, G is mid point of AD, hence, CD is parallel to BG, GCDB is parallelogram, diagonals bisect each other proving the ratio and concurrency

TheProles
Автор

Angle GBC should be equal to angle GEF(alternate angles) pls correct it int the video

object
Автор

there is a mistake, it is angle gef = angle gbc👍🏻

ALOK_KUMAWAT
Автор

Somewhat very slow teaching, make it little bit fast

rameshurade
Автор

Wrong proof you have made many mistakes there when I corrected them I got wrong result sorry but don't teach wrong🤥

mrdetective