filmov
tv
Computing an improper integral of the first kind.
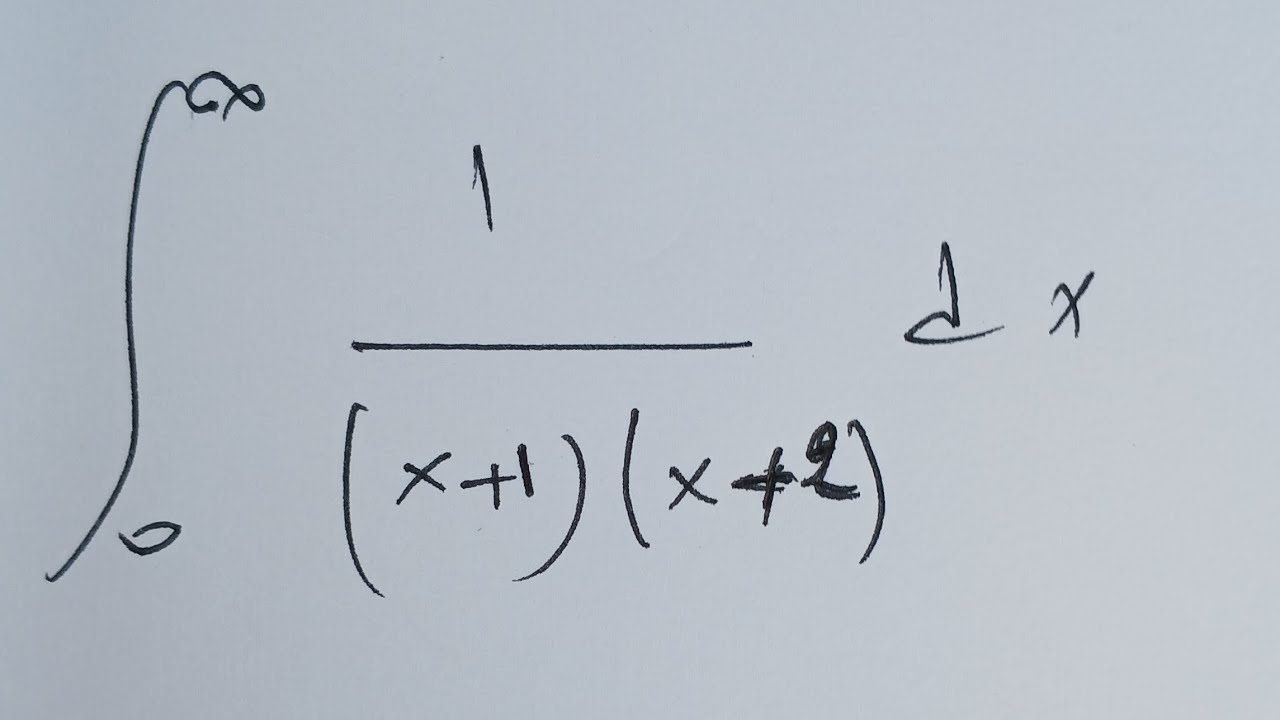
Показать описание
The difference between improper integral Is that it does have some meaning when we have f is positive. So before a definite integral We have a function that's defined on on some bonded interval. And with the finite Interval, a b and we assume that F doesn't have an infinite discontinuity, But in in Proper integral, We extend the concept of definite integral to the case where the interval is infinite And F has an infinite discontinuity on a b. So we can define the integral proper integral of the first kind when we did with Infinities in the bound.
So if the integral Of f of x between a and X exists for every number bigger than a, then we can Define the integral Between a and Infinity of f of x d x. And if it does exist and it's finite, we say that we have a convergent Integral And mostly we say the improper integral is convergent.
We will also Define the integral of the second kind. It's very important and we have the bounce problem and also we have the function discontinuities that you have to take care of it.
So if the integral Of f of x between a and X exists for every number bigger than a, then we can Define the integral Between a and Infinity of f of x d x. And if it does exist and it's finite, we say that we have a convergent Integral And mostly we say the improper integral is convergent.
We will also Define the integral of the second kind. It's very important and we have the bounce problem and also we have the function discontinuities that you have to take care of it.
 0:13:56
0:13:56
 0:12:24
0:12:24
 0:08:51
0:08:51
 0:03:52
0:03:52
 0:07:11
0:07:11
 0:03:35
0:03:35
 0:11:59
0:11:59
 0:23:17
0:23:17
 0:16:28
0:16:28
 0:10:02
0:10:02
 2:48:31
2:48:31
 0:35:59
0:35:59
 0:09:56
0:09:56
 0:36:04
0:36:04
 0:09:52
0:09:52
 0:00:16
0:00:16
 0:05:04
0:05:04
 0:06:04
0:06:04
 0:13:41
0:13:41
 0:28:56
0:28:56
 0:08:32
0:08:32
 0:06:34
0:06:34
 0:16:06
0:16:06
 0:10:23
0:10:23