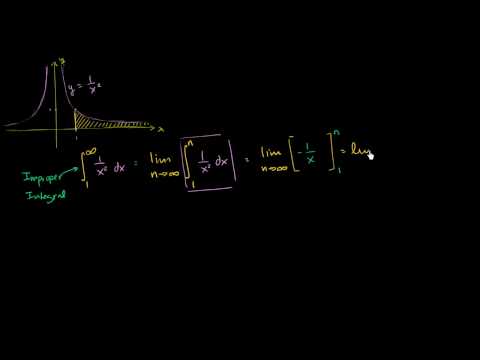
Introduction to improper integrals | AP Calculus BC | Khan Academy

Improper integrals are definite integrals where one or both of the _bounderies is at infinity, or where the integrand has a vertical asymptote in the interval of integration. As crazy as it may sound, we can actually calculate some improper integrals using some clever methods that involve limits. Created by Sal Khan.

AP Calculus BC on Khan Academy: Learn AP Calculus BC - everything from AP Calculus AB plus a few extra goodies, such as Taylor series, to prepare you for the AP Test

For free. For everyone. Forever. #YouCanLearnAnything

[Braeden]

You made me unerstand this in 3:51 minutes, my teacher only confused me in 2 hours 20 minutes.

[toribenita_kyo]

My calc prof asked us to calculate the area of the surface of y = sqrt(24-4x) revolved around the x-axis with an upper limit of 6 and a lower limit of 3. I was losing my patience with my calculator when it kept spitting out "math error" since 24-4(6) = 0. I ended up looking for help online to get the right answer. And then I figured out that I could have just plugged in instead of 6 to get a close-to-exact answer. It's a bit unorthodox, but it worked for me. I don't recommend doing it though. You want your calculations to be as true as possible. Only use shortcuts when you're absolutely desperate.

[GothGeekAnimeFreak]

Thank you thank you thank you for helping me pass my exam last

[bichpham]

thank you, this makes improper integrals much easier to understand :)))

[liptoncheetos]

With this corona thing my teacher just told us to to go here for maths.

[mrnosy]

Awesome video! It would be cool if you could do some introductory video's for QM involving normalizing the wave function using improper integrals of ±∞

[uzmashah]

Y'ALL. 1/n when n=infinity goes to zero because n can be any number like 5 or even 100. when you denominator is bigger than the numerator, it's a small number. 1/5 > 1/100. so as n gets larger, you get closer to zero. 1-0=1.

[whoknows]

bro come to my college here the teacher graduated from arts teach mathematics😂😂😂😂

[Juxtaroberto]

Exactly. The x value approaches a, or in this case M, but never equals that value, but the function equals its limit.

[pponcho]

This is mind blowing. How is infinity equal to exactly one. What math is this? Calculus?

[harveythrondsen]

Tomorrow I have final exams.And I learned all the definite, indefinite, improper integrals in 2 days.3 days ago I knew nothing about integral.Thanks to internet.

[bhavanimadasu]

Thank you sir Ur telling very clearly to understand the concept

[Juxtaroberto]

No, the area is exactly 1. N approaches infinity, but A=1.

[mrnosy]

yes calculus, but this doesn't mean infinity is exactly equal to one. We're just saying that as x approaches infinity starting from one, that since the function 1/(x^2) is getting closer and closer to a finite value as x approaches infinity that the area under the curve withing a certain boundary (1 to infinity) also approaches a finite value which can be written as (-1/n + 1). And since n approaches infinity on the bottom of the fraction the fraction will be infinitessimaly small so area = 1.

[TheDrBB]

Is there a Khan academy video about improper integrals when a function is discontinuous?

[Khana-Badosh-Official]

Bit confusion:
How can we get exact area 1 if we are evaulting with limit infinity???
I think it should be approximate value

[horaciosalgado]

yes, that's exactly right
type in your calculator 1/10 and 1/10000 and you will see that the bigger the denominator the closer it reaches 0.

[mTeeDev]

i think olevs right there. it approaches 1 not directly 1. but its so infinitely close to the 1 it is safe to say that it is 1. :)

[venzelzandrogabrielbaylan]

May I know what kind of app does he use on writing or making the solutions?

[lifeDotGov]

It doesn't approach 1, it IS 1. Limit doesn't mean it's approaching, if you learn the epsilon delta (precises) definition of a limit, you will see that it IS, not "approach"